CADmaster

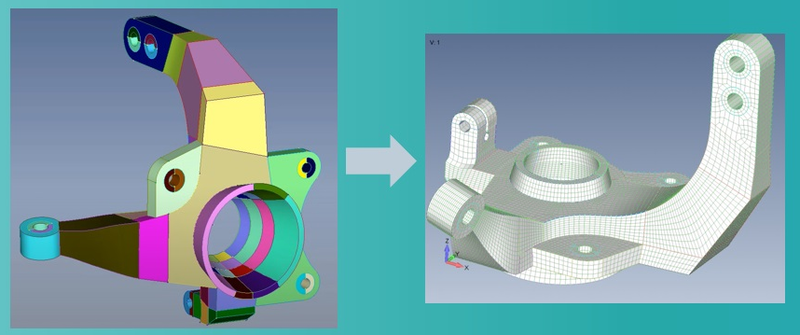
«Оптимальная расчетная конечно-элементная модель — какая она?» — такой чаще всего не проговоренный вслух, а порою даже и неосознанный вопрос непременно рождается (как минимум в подсознании) у каждого инженера-расчетчика при получении ТЗ на решение задачи методом конечных элементов (рис. 1). Каковы критерии этой самой расчетной модели-мечты? Пожалуй, здесь стоит отталкиваться от известного философского принципа «Всё следует упрощать до тех пор, пока это возможно, но не более того». Вот только как применить этот принцип к нашим научным и инженерным задачам?

Рис. 1

Критерии оптимальной расчетной конечно-элементной модели

Поразмыслив, проанализировав свой практический опыт, я выделил три основных критерия оптимальной расчетной конечно-элементной модели:

1. физические допущения, адекватные целям расчета;
2. упрощения детализации геометрии, правильный выбор видов конечных элементов и способов их соединения;
3. качественная сетка КЭ.

Эта статья является продолжением моего доклада «Особенности использования различных видов конечных элементов в Femap с NX Nastran», прочитанного на Femap Symposium 2020. В докладе я обзорно рассказывал о применении этих трех критериев на примере конкретных проектов, а здесь подробнее остановлюсь на втором критерии.

Чтобы определиться с концепцией рациональной расчетной схемы, в которую мы будем преобразовывать (чаще упрощать) исходную геометрическую модель, нужно в первую очередь хорошо понимать физику моделируемого процесса; знать, изменение каких факторов и параметров более всего влияет на результат. Необходимо разбираться в видах конечных элементов (линейные, поверхностные, объемные), способах соединения частей модели и в особенностях их совместного применения. Причем части модели могут состоять из конечных элементов разных видов. Да, и конечно же нужно знать возможности используемого вами расчетного комплекса. Расчетный комплекс Femap с NX Nastran поддерживает все виды конечных элементов и позволяет соединять области, состоящие из конечных элементов разных видов, всеми основными способами.

Способы соединения частей КЭ-модели

Существует три основных способа соединения (в более широком смысле слова — взаимодействия) частей конечно-элементной модели, передачи нагрузки и внутренних усилий между частями модели. Эта классификация носит условный характер, и я ввел ее для удобства восприятия информации расчетчиками-практиками.

Первый способ — соединение конечных элементов разных частей модели «узел в узел» (рис. 2). Это самый классический способ. При его использовании граница перехода между частями модели не оказывает никакого собственного влияния. Фактически решатель работает с единой сплошной моделью, а части модели существуют только для удобства работы пользователя в пре- и постпроцессоре.

Рис. 2

Второй способ — это применение MPC-связей (multiple point constraint). MPC соединяют узел с узлом (тогда это скорее SPC — single point constraint) или узел с группой узлов с помощью жестких или интерполяционных элементов (рис. 3).

Рис. 3

Третий способ — применение контактных поверхностей различных типов (например, «склейка» или «с трением»). При использовании этого способа пользователь выбирает контактирующие поверхности, а препроцессор автоматически определяет взаимодействующие узлы (рис. 4).

Рис. 4

Эти три способа соединения (взаимодействия) даже более чем различны. Например, целые классы задач (штамповка, соударение тел) просто невозможно решить без применения контактных поверхностей. При решении же более простых задач (линейная статика, модальный анализ), как правило, есть возможность выбрать, как именно упрощать геометрию и какой способ соединения частей модели применить.

Практические примеры

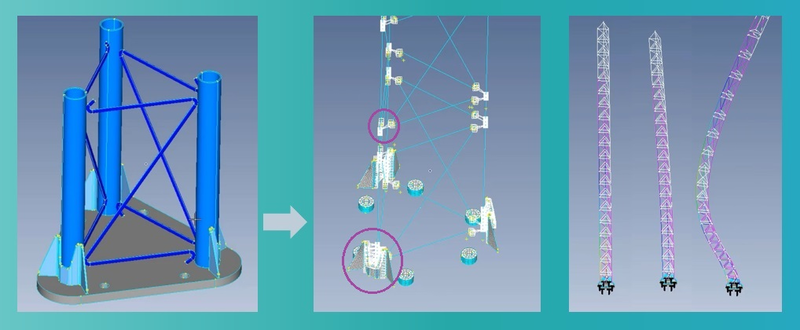
Разберем и проанализируем по вышеописанным критериям модель радиобашни, изображенную на рис. 3. Расчетная модель радиобашни используется для определения собственных форм и частот колебаний металлоконструкции башни, потому точный учет жесткости силовых элементов исключительно важен. Это очень ответственная задача — собственные частоты колебаний необходимы для определения динамической составляющей ветровой нагрузки (см. Руководство по расчету зданий и сооружений на действие ветра к СП 20.13  330.2010 «Нагрузки и воздействия»).

Модель радиобашни состоит из конечных элементов трех видов:

• несущие вертикальные круглые трубы и связи соединяющих (также из круглых труб) смоделированы балочными конечными элементами;
• ребра жесткости, соединяющие трубы и опорную плиту, смоделированы поверхностными КЭ;
• опорная плита смоделирована солидами (объемными КЭ).

В модели также применены три основных способа соединения частей конечно-элементной модели:

• узел в узел соединены части модели (линейные), между которыми нет зазоров;
• с помощью MPC-связей соединены линейные элементы (имитирующие трубы), между которыми есть зазоры. Кроме того, посредством MPC-связей соединены элементы ребер жесткости и вертикальных труб;
• контакты заданы между нижней гранью ребер жесткости и поверхностью опорной плиты.

Я считаю эту расчетную модель очень грамотным результатом преобразования геометрической модели в расчетную, так как модель достаточно проста, но при этом в ней учтены основные конструктивные элементы, определяющие жесткость конструкции. Как правило, в простых строительных САПР отсутствуют инструменты, позволяющие соединять конечные элементы различных видов (в случае радиобашни не было бы возможности смоделировать опорные элементы). То есть в простой строительной САПР конструкцию радиобашни удалось бы смоделировать лишь из одних труб, разбив их балочными конечными элементами. В этом случае податливость основания не учитывается и собственные частоты колебаний конструкции оказываются завышены.

Далее на примере расчетного комплекса Simcenter Femap c NX Nastran я подробнее расскажу о втором способе соединения частей модели, а точнее о применении MPC-связей. Элементы типа R математически эквивалентны многоточечному уравнению связи (Multipoint Constraints Equations, MPC). Они накладывают постоянные ограничения на компоненты перемещения соединяемых узлов. Каждое уравнение связи выражает зависимую степень свободы как функцию независимой степени свободы.

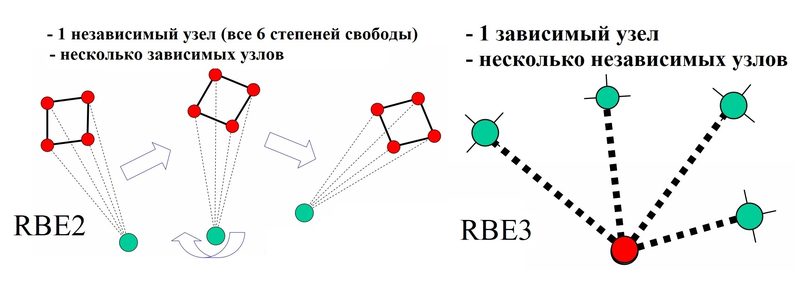
Элементы RROD, RBAR, RBE1, RBE2 и RTRPLT — это жесткие элементы. Элементы RBE3 и RSPLINE — интерполяционные, они не являются жесткими (рис. 5).

Рис. 5

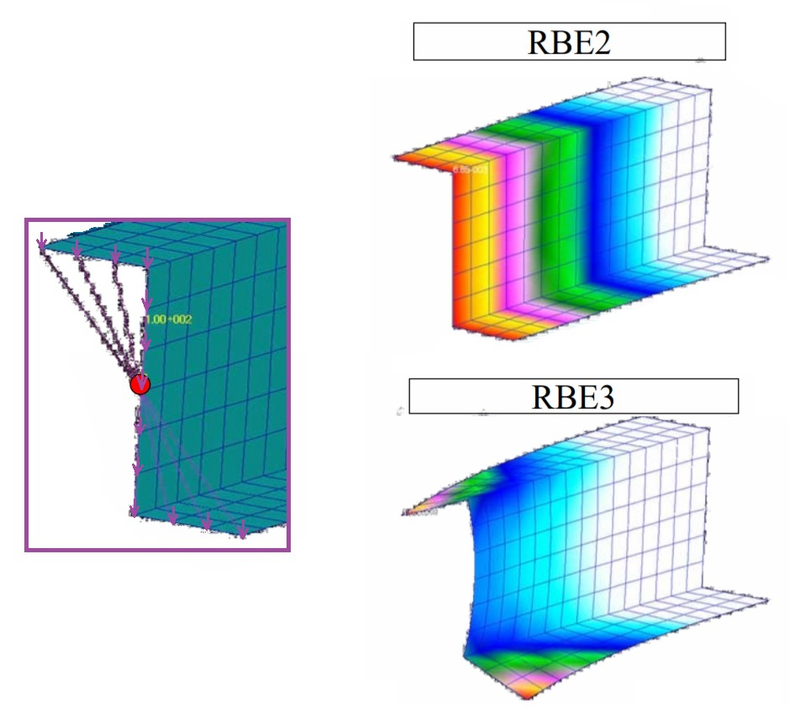
Элемент RBE2 использует уравнения связи, чтобы связывать степени свободы зависимых узлов со степенями свободы независимого узла. Относительные деформации между зависимыми узлами отсутствуют, то есть соответствующие элементы не деформируются. Варьируя настройки степеней свободы RBE2 в поле Dependent (Зависимый), можно получить WELD — сварное соединение (активируя шесть степеней свободы TX, TY, TZ, RX, RY, RZ) или BOLT — болтовое соединение (активируя TX, TY, TZ, вращения остаются свободными).

В отличие от элементов RBE2, элемент RBE3 не добавляет конструкции дополнительную жесткость, то есть RBE3 — это интерполяционный элемент. RBE3 можно использовать как инструмент распределения нагрузки и массы в КЭ-модели, аналогичный «грузовым площадям» в строительных системах автоматизированного проектирования. Нагрузки в виде сил и моментов, приложенные к зависимому узлу, распределяются в независимые узлы пропорционально весовым коэффициентам (рис. 6).

Рис. 6

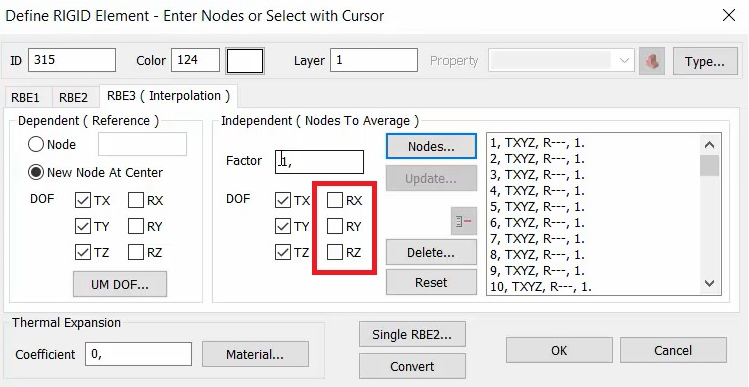
Для большинства случаев в настройках степеней свободы RBE3 в поле Independent (Независимый) не рекомендуется активировать вращательные степени свободы (рис. 7).

Подробнее специфика применения RBE2 и RBE3 представлена в статье наших партнеров из компании «КАДИС»: «RBE2 в сравнении с RBE3 в Femap c NX Nastran».

Рис. 7

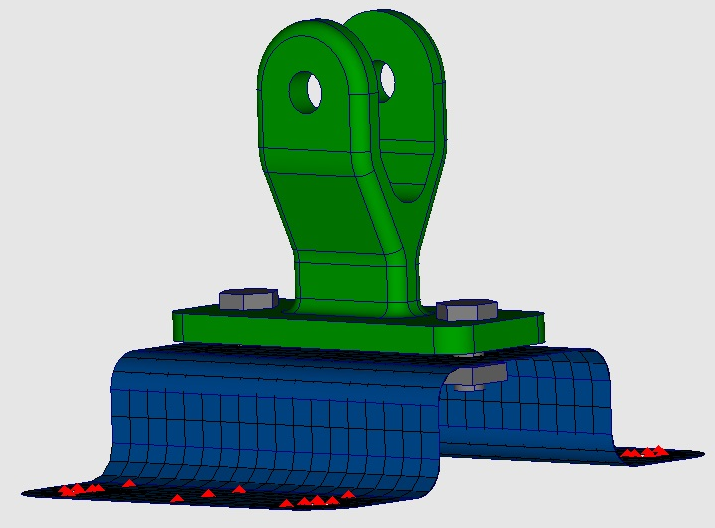
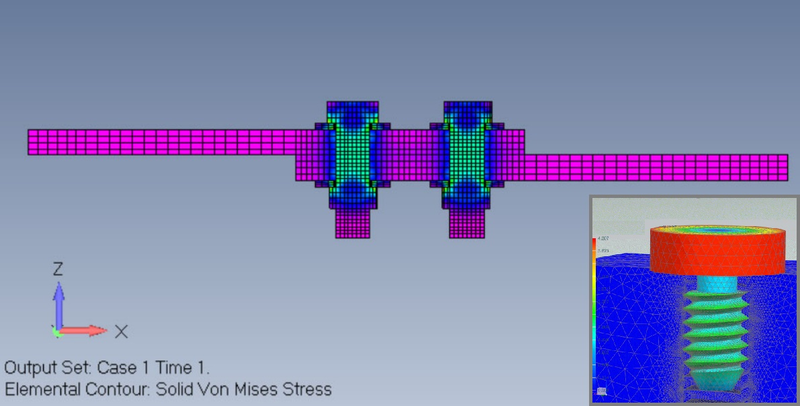
Но вернемся от теории к практике и разберем типовую задачу расчета кронштейна, на примере которой отлично видно, что, неправильно задав способ соединения частей модели, мы получим принципиально неверное решение. Кронштейн закреплен на П-образной пластине с помощью двух болтов. К отверстиям кронштейна приложена сила с направлением вдоль пластины. П-образная пластина разбита поверхностными конечными элементами, а кронштейн — объемными КЭ. С учетом толщины пластины пластина и кронштейн соприкасаются (рис. 8).

Рис. 8

Чтобы результат расчета был адекватен, способ соединения кронштейна с П-пластиной (модель передачи нагрузки) должен соответствовать реальной физике работы болтового соединения. Гайки закручены с некоторым усилием (моментом). Этот момент вызывает силу, прижимающую кронштейн к поверхности пластины. Силу трения в свою очередь определяют коэффициент трения и сила реакции. При приложении нагрузки к кронштейну часть его основания прижимается к пластине, а некоторая часть, напротив, стремится от него оторваться, вследствие чего при превышении определенной нагрузки происходит частичное раскрытие стыка.

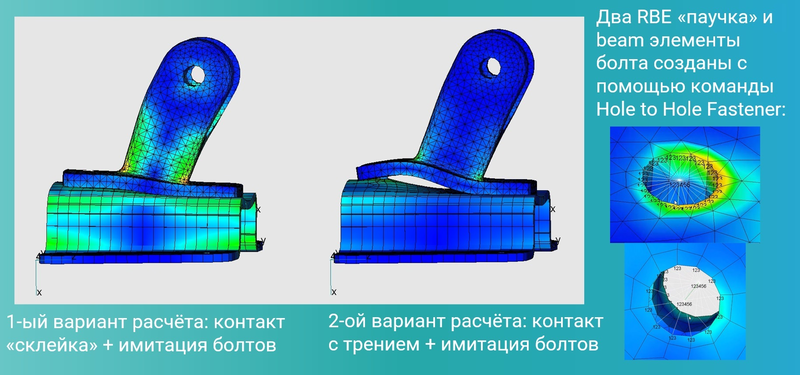
С точки зрения математического моделирования нам необходимо: а) задать непосредственное соединение болтов и гаек с кронштейном и пластиной и б) задать взаимодействие изначально прижатых друг к другу поверхностей. На рис. 9 показаны напряженно-деформированные состояния кронштейна с пластиной при двух вариантах задания соединений. Составляющая а — назовем ее «имитация болтов» — в обоих вариантах задана одинаково: два «паучка» из RBE-элементов и болт из балочных конечных элементов созданы с помощью встроенной API-команды Hole to Hole Fastener.

Первый и второй варианты различаются настройками свойств контактной пары поверхностей — составляющей б. В первом варианте настройки контакта соответствуют «склейке» двух поверхностей, что не отвечает физике работы болтового соединения. Этот вариант можно было бы использовать, если бы кронштейн был соединен с пластиной при помощи сварных швов — по периметру и внутри. Адекватное решение (второй вариант расчета) получается при задании контакта с трением. Такой вид взаимодействия поверхностей позволяет учесть эффект частичного раскрытия стыка. Задача при этом становится нелинейной и требует гораздо больше времени в связи с необходимостью обеспечить сходимость решения. Подробнее о нелинейном анализе и обеспечении сходимости можно прочитать в моей статье «Просто о нелинейном анализе методом конечных элементов. На примере кронштейна».

Рис. 9

Существует несколько способов моделирования болтового соединения. Представленный выше способ (балочный элемент + RBE + контакт с трением) относительно прост, однако он позволяет учесть передачу сдвиговых усилий. Есть более точный, но и гораздо более трудоемкий способ моделирования болтового соединения: непосредственное моделирование болтов, гаек, шайб объемными конечными элементами (рис. 10). Этот способ позволяет учесть все тонкости работы болтового соединения (даже контакт в резьбе) и в том числе производить нелинейный анализ с учетом пластичности.

Рис. 10

Глобально-локальный анализ

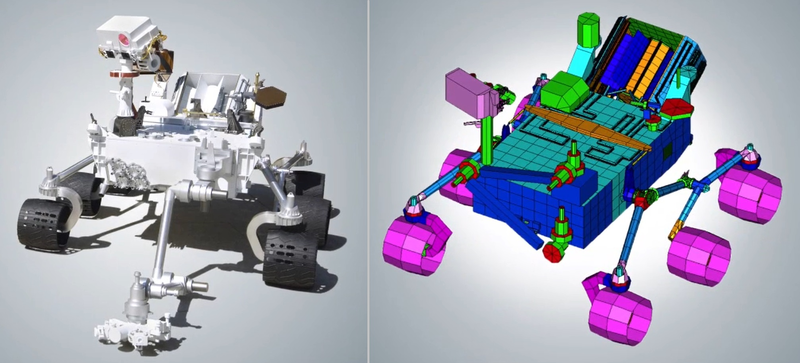
Проанализируем теперь сложную конечно-элементную модель марсохода «Кьюриосити» («Curiosity»). На примере марсохода я хочу познакомить читателя с понятием глобально-локального анализа (ГЛА). Глобально-локальный анализ — это процесс изолированного рассмотрения отдельных частей конструкции, при котором выполняется условие равенства силовых факторов и перемещений, соответствующих поведению этой части в составе конструкции. Возможность применения ГЛА обоснована принципом Сен-Венана: в частях конструкции, достаточно удаленных от места приложения нагрузки, напряжения и деформации мало зависят от способа приложения нагрузки. Потому часть модели можно вырезать и выполнить анализ только для этой части — при условии, что значения силовых факторов на границах выреза заданы правильно.

Рис. 11

Но вернемся к марсоходу и его модели. Весит марсоход около тонны, его габариты: длина — 4,5 метра, ширина — 2,5 метра, высота — 2,1 метра. В процессе проектирования было проведено множество расчетов средствами Simcenter Femap, в том числе линейный статический анализ, анализ потери устойчивости, нелинейный анализ; рассчитаны отклики на воздействие случайной вибрации, выполнен анализ переходных процессов.

Конечно-элементная модель марсохода, изображенная на рис. 11, — это глобальная конечно-элементная модель (ГКЭМ). С ее помощью можно подобрать сечения труб и толщины оболочек, вычислить нагрузки — реакции в узлах конструкции. В модели применены линейные, поверхностные и объемные КЭ, части модели соединяются как «узел в узел», так и посредством MPC-связей и контактов. Для такой сложной конструкции, как марсоход, рационально использовать глобальную модель как нагрузочную, а узлы считать отдельно с помощью подробных локальных конечно-элементных моделей (ЛКЭМ) — то есть применять алгоритм глобально-локального анализа (рис. 12).

Для расчета узлов в ЛКЭМ очень важно правильно задать граничные условия, силовые факторы. Существует три способа переноса граничных условий из ГКЭМ в локальную конечно-элементную модель: перенос перемещений, перенос силовых факторов, комбинированный способ. Для осуществления этих операций в Femap есть удобный инструмент FreeBody. Чтобы более подробно узнать о ГЛА и о применении FreeBody, рекомендую ознакомиться с докладом Алексея Патая из компании «Центр Технических Проектов»: «Возможности Femap для глобально-локального анализа авиационных конструкций».

Рис. 12

Заключение

Подведем итоги, опираясь на вышеприведенные результаты анализа трех расчетных моделей: радиобашни, кронштейна и марсохода. Какая она все-таки — оптимальная расчетная конечно-элементная модель, и насколько простой модель может быть? Ответ для каждой конкретной задачи индивидуален, но есть общие критерии.

Что касается понимания физики процесса: например, нам не нужно моделировать каждый крепежный элемент радиобашни, чтобы определить собственные формы и частоты колебаний конструкции, — требуется учитывать лишь элементы, в целом определяющие распределение масс и жесткость конструкции.

Для подбора сечений в строительных расчетах (металлоконструкции, деревянные конструкции и даже часть железобетонных), где чаще всего можно ограничиться использованием только линейных конечных элементов, достаточно понимать, является ли узел условно «жестким» или условно «шарнирным». Условно — потому как в любом «шарнирном» узле есть трение, а любой «жесткий» узел все равно имеет некоторую податливость. Для моделирования течений жидкости или газа, с точки зрения геометрической модели, и вовсе достаточно задать поверхность обтекаемого объекта. Так, например, геометрическая модель для определения буксировочного сопротивления судна — это прямоугольный параллелепипед, из которого вычтен объем корпуса судна.

На примере расчета кронштейна, соединенного болтами с П-образной пластиной, мы увидели, что очень важно правильно задать способ передачи нагрузки, граничные условия. В противном случае мы получим результат, не соответствующий действительности. Да, в соответствии с принципом Сен-Венана, напряженно-деформированное состояние (НДС) конструкции в глобальной модели на достаточном удалении от неточно смоделированного узла практически не изменится. Но НДС элементов узла будет определено неверно, что может быть критичным, если это ответственный узел и он сильно нагружен. Особенно важно — как для точности решения, так и для сходимости — правильно задавать нелинейные контакты.

Для сложных же конструкций, таких как марсоход «Кьюриосити», делать одну сложную и подробную конечно-элементную модель чаще всего нерационально. Целесообразнее использовать алгоритм глобально-локального анализа, то есть формировать глобальную нагрузочную конечно-элементную модель и локальные конечно-элементные модели для расчета ответственных узлов. Затем, после расчета узлов, при необходимости можно внести изменения-уточнения в ГКЭМ.

Конечно, тема оптимальной расчетной конечно-элементной модели не может быть исчерпана в рамках одной статьи. Но я надеюсь, что мой обобщенный практический опыт и теоретические знания будут полезны, и в следующий раз вы сможете быстрее найти свое оптимальное решение. При этом расчетная модель будет проще, а точность выше!

Бесплатную пробную версию Simcenter Femap с NX Nastran можно скачать по адресу solidrules.ru/simcenter-femap.

Скачать статью в формате PDF — 4.15 Мбайт