CADmaster

В ходе работы над новой версией программы «Гидросистема» авторы еще раз убедились в справедливости известных афоризмов «Мы ленивы и нелюбопытны» и «Новое — это хорошо забытое старое».

В процессе работы над реализацией расчета газо-жидкостного течения возникла необходимость решить следующие задачи:

• расчет фазового равновесия по заданному давлению и энтальпии, по заданному давлению и по массовому газосодержанию;
• определение места перехода двухфазного течения в однофазное и обратно (точки начала кипения или конденсации).

В конечном итоге обе эти задачи свелись к нахождению изолированного корня нелинейного уравнения вида

на интервале 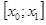, где f; - гладкая монотонная функция.

Казалось бы, в чем проблема? Ведь это основа любого вузовского курса численных методов. И первое, что приходит на ум — применить классический метод Ньютона (см., например, [1]). Но не тут-то было… Метод Ньютона требует вычисления производной функции f;, что для решения наших задач крайне трудоемко или вообще невозможно. И такая ситуация достаточно типична для вычислительных инженерных задач.

Какие еще методы, не требующие расчета производной, предлагают нам вузовские учебники? Их набор обычно стандартен:

• метод половинного деления;
• метод простых итераций;
• метод секущих;
• метод хорд.

Сходимость метода простых итераций, метода секущих, да и метода Ньютона не гарантирована и зависит от начального приближения и характера функции f;. Поэтому применение этих методов в коммерческой программе — не самый желательный вариант.

Метод половинного деления и метод хорд гарантируют сходимость к искомому решению, однако их эффективность в ситуации, когда расчет каждого значения функции f; требует больших вычислительных ресурсов, невысока.

Напомним, что эффективность метода обычно характеризуют порядком сходимости. Число p называют порядком сходимости, если в области сходимости имеет место оценка 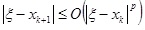, где 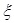- корень уравнения, x_k — значение x, полученное на шаге k. Очевидно, что метод половинного деления имеет линейный порядок сходимости (p=1), в то время как метод Ньютона — квадратичный порядок (p=2).

Каждый шаг метода может требовать расчета не одного, а n значений функции f; или ее производных. Если такие вычисления трудоемки, имеет смысл сравнивать не порядки сходимости, а (следуя Траубу [4]) так называемый индекс эффективности метода, показывающий средний порядок сходимости, который приходится на один расчет функции. Данный показатель равен 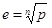, где p — порядок сходимости, — число вычислений функции или ее производных на одном шаге. Таким образом, индекс эффективности метода половинного деления — e=1, а метода Ньютона — .

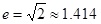Что касается метода хорд (называемого в англоязычной литературе методом ложного положения — «regula falsi»), то он тоже имеет линейный порядок сходимости и по эффективности не превосходит метод половинного деления (p=1,e=1). Это связано с тем, что итерации в данном методе имеют тенденцию приближаться к корню уравнения только с одной стороны [1, стр. 93].

Возникает вопрос: неужели не существует метода, гарантирующего сходимость, но значительно более эффективного, чем описанные в учебниках? Оказывается, такие методы были придуманы уже более 30 лет назад. Один из самых простых и в то же время очень эффективных и надежных из них — так называемый улучшенный метод Pegasus. Он модифицирует метод хорд таким образом, чтобы последовательность приближений «перепрыгивала» исходный корень как можно чаще, беря его, как выражаются артиллеристы, «в вилку». Для этого метод хорд на большинстве шагов применяется к скорректированному значению функции, что обеспечивает как можно более точный «перелет» через корень. Ниже приведена формулировка алгоритма.

Алгоритм использует следующие переменные:

x^* — текущее приближение для искомого значения;

x^** — предыдущее приближение для искомого значения;

x_L, x_R — текущие границы интервала, где расположен нуль функции (x_L<x^*<x_R);

y^*, y^** — значение функции для текущего и предыдущего приближения;

y_L, y_R — значения, используемые для вычисления следующего приближения и соответствующие концам интервала (они не обязательно совпадают со значениями функции в ходе алгоритма и могут быть намеренно изменены!); в нашем случае в ходе алгоритма всегда y_L<0,y_R>0;

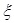- заданная допустимая погрешность (отклонение функции от нуля).

Предполагается, что функция f; возрастает (в противном случае достаточно применить алгоритм к функции -f;).

Шаг 1 — простая линейная интерполяция

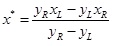, y^*=f;(x^*)
Если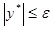 - конец, возвращаем значение x^* в противном случае — переход к шагу 2.

Шаг 2 — усовершенствованная интерполяция методом Pegasus

x^**=x^*,y^**=y^* (запоминаем предыдущее приближение).

Если y^*>0,

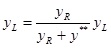
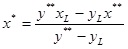y^*=f;(x^*)

Если — конец, возвращаем значение, в противном случае — x_L=x^**,y_L= y^**.

При y^*<0 — повтор шага 2; при, y^*>0 x_r=x^*y_r=y^* -переход к шагу 1.

В статье [2] доказывается, что индекс эффективности данного алгоритма не меньше, то есть существенно выше, чем у метода Ньютона! А в статье [3] предлагаются более сложные варианты алгоритмов (на основе усовершенствования алгоритмов подобного же типа, а также алгоритма квадратичной аппроксимации Мюллера), у которых индекс эффективности достигает !

За прошедшие с момента появления работ [2, 3] тридцать с лишним лет было предложено множество самых оригинальных и изощренных методов для решения уравнения (1). Но, насколько известно авторам, ни один из алгоритмов по сочетанию надежности и индекса эффективности не превзошел методов, изложенных в [2, 3].

Результаты применения усовершенствованного алгоритма Pegasus в программе «Гидросистема» приведены в таблице. Как видим, этот алгоритм позволяет более чем вдвое ускорить работу!

Таблица. Сравнение метода половинного деления и усовершенствованного метода Pegasus по числу итераций

		Число итераций
Задача	Абсолютная точность поиска корня	Метод пол. дел.	Pegasus
Расчет температуры смеси по заданным давлению и энтропии для двухфазного потока	1E-3	16	6
	1E-5	23	9
	1E-7	29	11
Задача пересчета массового газосодержания в мольное	1E-3	9	5
	1E-5	16	7
	1E-7	20	10
Определение места фазового перехода в трубопроводе	1E-3	12	6
	1E-5	18	8
	1E-7	23	11
Итого:		166	73

Почему же столь простой, надежный и высокоэффективный алгоритм не изучается в вузовских курсах численных методов? Вопрос, как говорится, риторический…

Литература

1. Гартман Т.Н., Клушин Д.В. Основы компьютерного моделирования химико-технологических процессов. Учебное пособие для ВУЗов. — М., ГКЦ «Академкнига», 2006.
2. King R.F. An improved Pegasus method for root finding. — BIT 13, 423−427, 1973.
3. King R.F. Methods without secant steps for finding a bracketed root. — Computing 17, 1976.
4. Traub, J.F. Iterative methods for the solution of equations, 310pp. — Prentice-Hall, Englewood Cliffs, New Jersey, 1964.