CADmaster

При проектировании ответственных сооружений, в особенности когда применяются относительно новые конструктивные решения, часто возникает необходимость расчета некоторых ключевых фрагментов конструктивного комплекса. Речь при этом идет не о выполнении стандартного проектировочного расчета, а о параметрическом исследовании, детализация которого намного превышает стандартный уровень. Ниже представлен пример такого исследования, выполненный средствами вычислительного комплекса SCAD.

Необходимость проанализировать напряженно-деформированное состояние опорного железобетонного узла радиальной фермы покрытия была продиктована новизной предложенного конструктивного решения. Сложность конструкции узла и, как следствие, сложность возникающего в нем напряженно-деформированного состояния, обеспечение несущей способности узла требуют качественного анализа распределения напряжений и усилий — с оценкой обоснованности назначенного армирования и размеров бетонного сечения.

При расчетном анализе прежде всего устанавливалось распределение потока внутренних усилий (напряжений) в местах передачи на железобетонную конструкцию стены больших сосредоточенных сил (то есть в местах опирания радиальной стальной фермы покрытия).

С учетом важности рассматриваемого опорного узла при анализе его напряженно-деформированного состояния использовались следующие расчетные модели:

• укрупненная пространственная расчетная модель железобетонной конструкции блока трибун;
• пространственный фрагмент расчетной модели железобетонной конструкции блока трибун в местах опирания стальной радиальной фермы;
• плоский фрагмент расчетной модели железобетонной конструкции блока трибун в местах опирания стальной радиальной фермы;
• пространственный фрагмент расчетной модели железобетонной конструкции блока трибун в местах опирания стальной радиальной фермы, составленный с использованием нелинейной характеристики работы бетона.

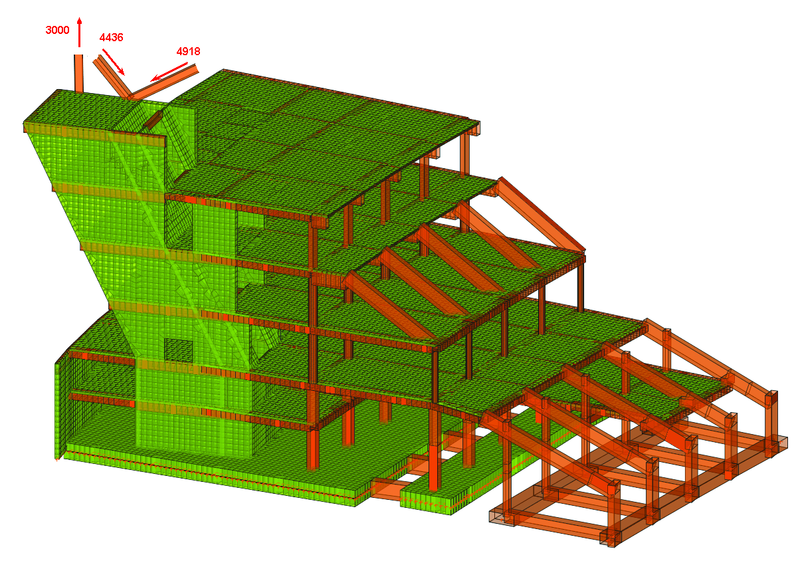
Модель железобетонной конструкции блока трибун (рис. 1) предназначена для определения напряженно-деформированного состояния его полной расчетной схемы — от постоянных, технологических, снеговых и ветровых нагрузок на сам блок и покрытие, которое опирается на этот блок.

При выполнении расчета укрупненной пространственной модели блока были приняты повышенные нагрузки от покрытия (Р₁ = 3000 т, Р₂ = 4436 т, Р₃ = 4918 т). В дальнейшем из полной схемы был выделен для подробного расчета и анализа фрагмент исследуемого участка конструкции.

Рис. 1. Укрупненная расчетная модель блока трибун

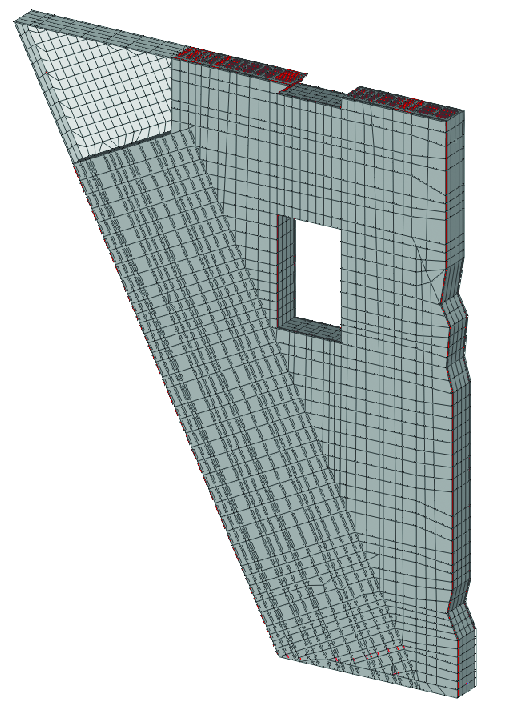
Этот фрагмент предназначен для подробного анализа напряженно-деформированного состояния участка опоры в местах опирания фермы покрытия. Поскольку в непосредственной близости от исследуемого участка конструкции предусмотрено создание отверстий в стене, было принято решение включить в анализ взаимодействие с отверстием, что и предопределило размер фрагмента конструкции (рис. 2). Выделение произведено методом фрагментации [1], для чего с помощью функции Нагрузка от фрагмента схемы, реализованной в программном комплексе SCAD [2], были определены все усилия взаимодействия между выделенным фрагментом и остальной частью схемы.

По толщине стены конечно-элементная расчетная модель узла была составлена из пяти слоев трехмерных конечных элементов, с помощью которых моделировалась работа бетона, и из стержневых элементов, которыми моделировались работа арматуры и анкерные болты. Мощные стальные закладные детали, передающие нагрузки от покрытия на бетон и анкерные узлы, моделировались бесконечно жесткими телами.

Стержневые элементы ориентировались по направлению расположения арматуры, но их количество не соответствовало реальному числу арматурных стержней, поэтому продольная жесткость EF подбиралась такой, чтобы соответствовать реальной жесткости пучка стержней арматуры на соответствующем участке конструкции. Стержни, моделирующие арматуру (в отличие от стержней, моделирующих анкерные болты), присоединялись ко всем узлам конечно-элементной модели, моделируя тем самым совместную работу арматуры и бетона без проскальзывания. Анкерные стержни присоединялись к верхней и нижней анкерным плитам.

При расчете пространственного фрагмента была разработана детальная трехмерная конечно-элементная расчетная модель узла опирания покрытия (рис. 2а), находящегося в самоуравновешенном состоянии под действием сил взаимодействия и нагрузок от покрытия (рис. 2б).

По результатам расчета были получены значения реакций во внешних связях, практически равные нулю, а картина напряженно-деформированного состояния (НДС) узла показала следующее:

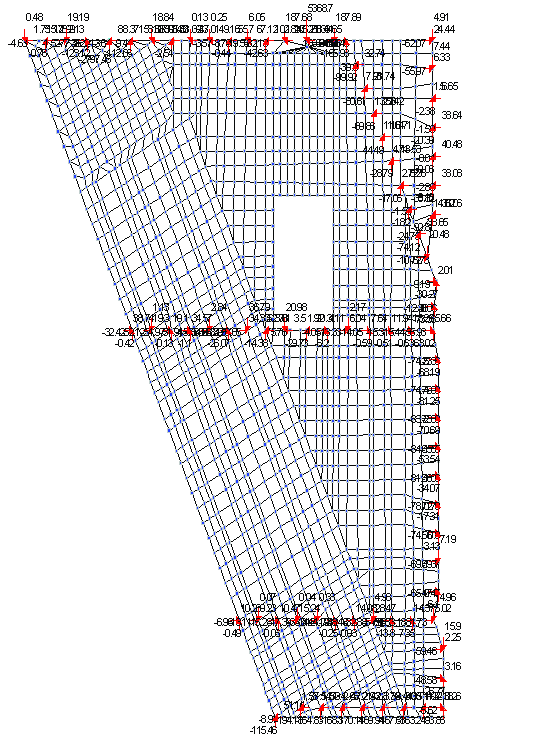
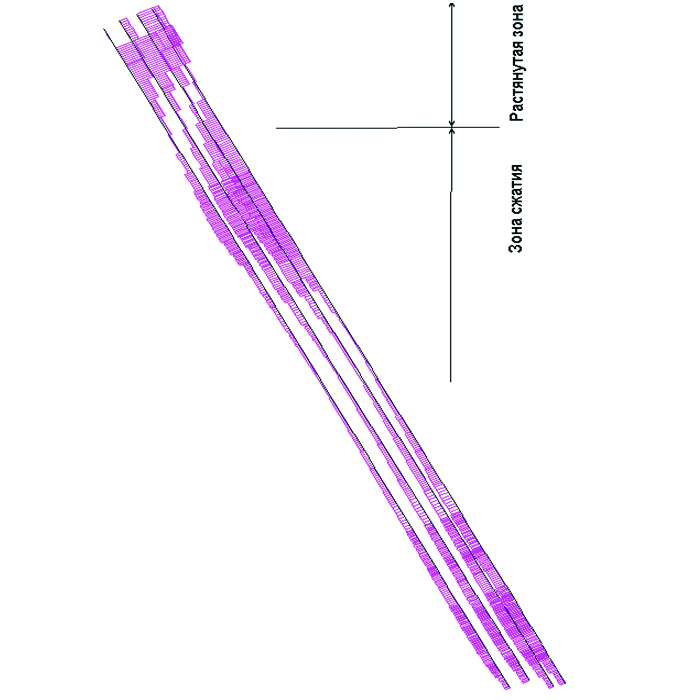
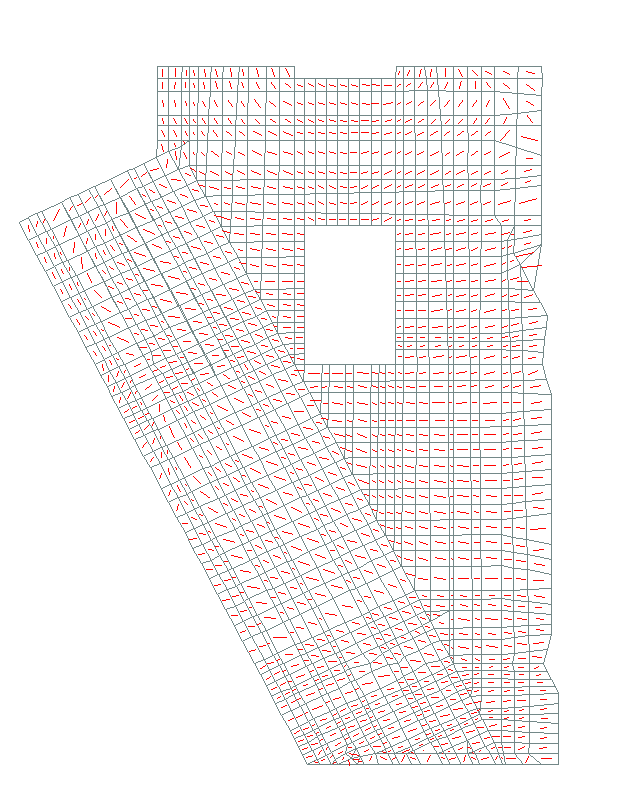
1. не подтвердились предположения проектировщиков о передаче горизонтальной компоненты усилий на бетон по центру вертикальной площадки и о равномерной передаче усилий на анкерные болты. На это указывает поворот закладной детали (рис. 3), образование клиновидной щели между закладной деталью и бетоном стены, а также неравномерное распределение усилий в анкерных болтах (рис. 4);
   Рис. 3. Деформированное состояние (масштаб перемещений увеличен)
   Рис. 4. Распределение усилий в анкерных болтах
   </дш>
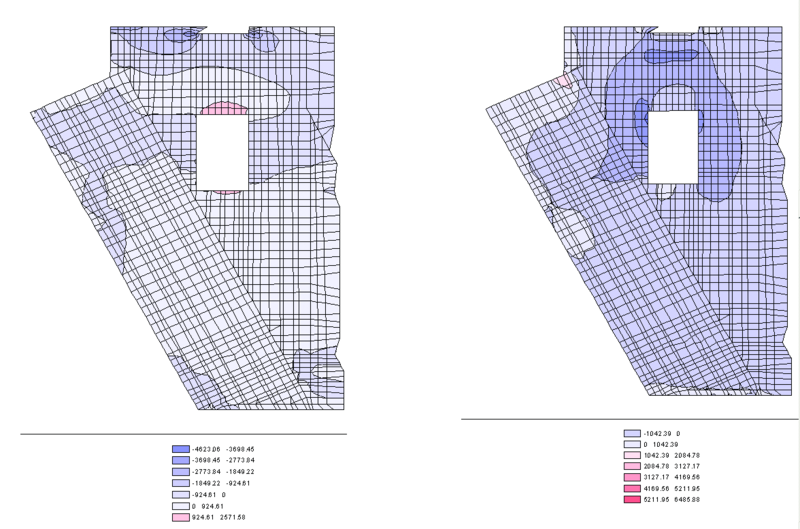
2. бетон в исследуемом районе в основном оказался сжатым (рис. 5), через это сжатие он передает усилие с нижней анкерной плиты на внешнее армирование. Зоны растяжения, где можно ожидать появления трещин, относительно невелики;
3. внешняя арматура растянута только в верхней зоне. В других местах, расположенных под нижней анкерной плитой, эта арматура включается в работу стены на сжатие (рис. 6);
4. по толщине стены НДС меняется весьма незначительно.

На основе результатов расчета трехмерной модели и с учетом однородности этой модели по толщине была сформирована двумерная расчетная модель, которая позволила отследить направления главных растягивающих напряжений (схему трещинообразования), а также выполнить проверку армирования.

Двумерная модель набрана из конечных элементов плоского напряженного состояния и стержневых элементов. Последними (как и в трехмерной модели) моделировались анкерные болты и арматура, элементы плоского напряженного состояния моделируют работу бетона. При построении модели все стержни, моделирующие арматуру и анкерные болты, были приведены к одной плоскости.

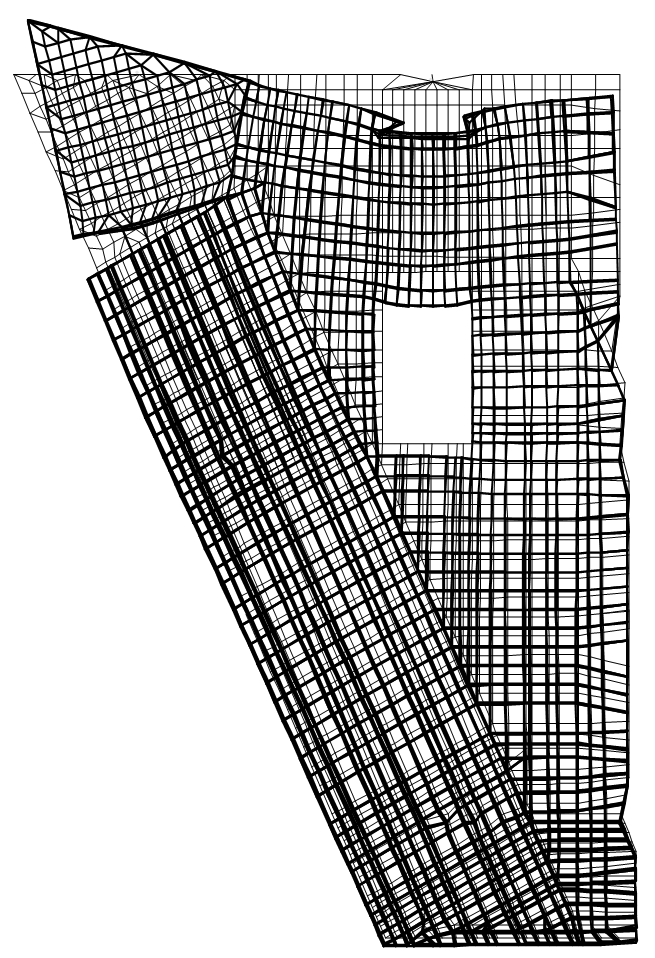
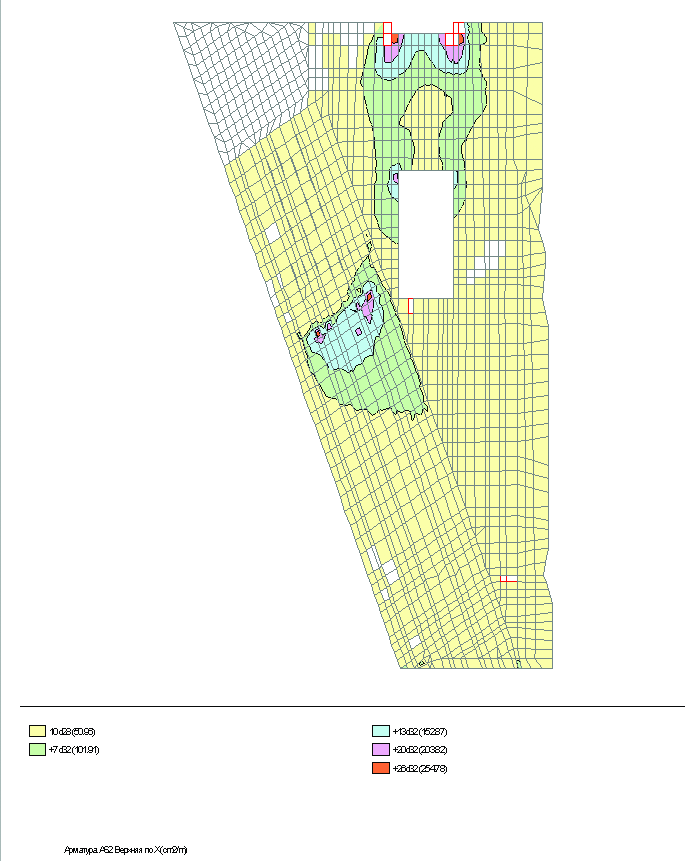
Расчет плоской модели показал схему ориентации площадок, по которым действуют максимальные по модулю главные напряжения (рис. 7). Кроме того, в этой модели была подобрана арматура (рис. 8): она оказалась меньшей по площади, но близкой по значениям к той, которая предусмотрена авторами проекта.

Рис. 5. Напряжения в бетоне: а — на вертикальных площадках (sx); б — на горизонтальных площадках (sz)

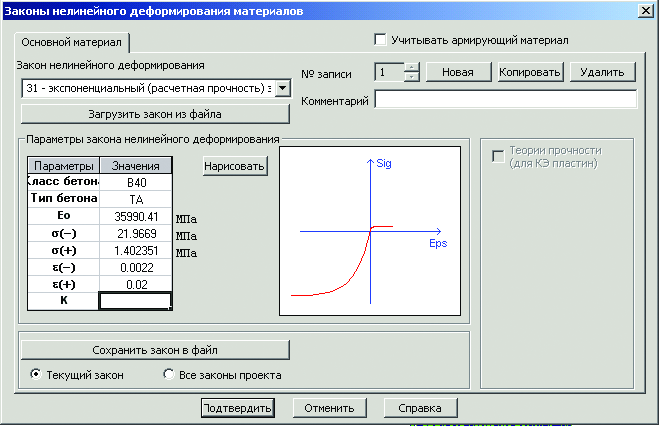
Для получения дополнительных данных о напряженно-деформированном состоянии узла был выполнен расчет модели с использованием для моделирования бетона типа жесткости, учитывающего нелинейную работу материала (нелинейную диаграмму «деформация — напряжение») (рис. 9). При выполнении этого расчета использовался программный комплекс «Лира» (версия 9.4) [3].

Расчет выполнялся пошагово, с контролем напряжений и деформаций на каждом шаге расчета. Использование такого расчета позволяет достаточно обоснованно учесть изменение модуля деформирования в зависимости от действующих напряжений, а также исключить из работы бетонные элементы, растягивающие напряжения в которых превышают расчетное сопротивление бетона растяжению, и разрушающиеся при сжатии (если такие появятся).

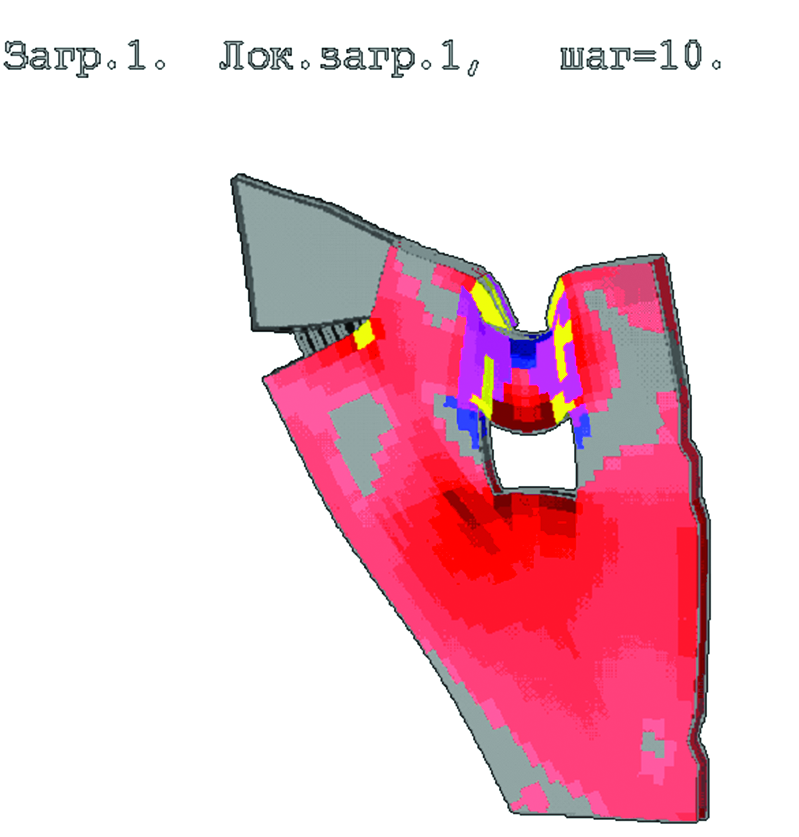
На рис. 10 и 11 приведено распределение напряжений, полученных в результате расчета, а на рис. 12 показаны изополя участков, на которых превышено значение расчетного сопротивления бетона растяжению.

Рис. 10. Распределение вертикальных напряжений Рис. 11. Распределение горизонтальных напряжений (вдоль Х)

Как видно на иллюстрациях, полученные при расчете значения напряжений и зон, требующих армирования, достаточно хорошо согласуются с результатами линейных расчетов на основе как трехмерной, так и плоско-напряженной (двумерной) расчетных схем.

При этом:

• напряжения в арматуре не превысили расчетного сопротивления арматуры на растяжение;
• напряжения в бетоне (за исключением мест концентрации усилий) не превышают расчетного сопротивления бетона на сжатие, а значения деформаций в бетоне — своих предельных значений при сжатии. На это указывает отсутствие зон разрушения бетона при сжатии;
• отсутствие зон разрушения бетона вдоль арматурных стержней указывает на обеспечение совместной работы бетона и арматуры.

Выводы

1. Вариантные расчеты моделей узла опирания радиальной фермы покрытия позволили получить достаточно полные данные о его напряженно-деформированном состоянии.
2. Анализ результатов расчетов показал следующее:
   • распределение усилий и деформаций в месте крепления растянутой стойки фермы несколько отличается от предусмотренного проектом. На это указывает поворот опорной металлической пластины. Выявленное отличие не является критерием надежности работы узла, а требует лишь учета при оценке работы узла, что и было сделано в расчетах;
   • содержание армирования в узле (по направлению и количеству) соответствует распределению напряжений, полученному при расчете;
   • напряжения в бетоне не превышают расчетного сопротивления бетона на сжатие;
   • обеспечена совместная работа бетона и арматуры в узле.
3. Качественная оценка напряженно-деформированного состояния опорного железобетонного узла радиальной фермы покрытия стадиона подтверждает обоснованность его конструктивных решений.
4. Узел запроектирован на восприятие нагрузок от покрытия, которые примерно на 30% превышают проектные. Можно утверждать, что проектные решения приняты в запас надежности узла.
5. Учитывая появление клиновидного зазора между закладной деталью и железобетонной стеной (рис. 3), омоноличивать это место нецелесообразно, поскольку здесь в бетоне омоноличивания возможно раскрытие трещин.

Литература

1. Перельмутер А.В., Сливкер В.И. Расчетные модели сооружений и возможность их анализа / Изд. 3-е, переработанное и дополненное. — М.: ДМК Пресс, 2007. — 600 с. (Серия «Проектирование»).
2. Карпиловский В.С., Криксунов Э.З., Маляренко А.А., Микитаренко М.А., Перельмутер А.В., Перельмутер М.А. SCAD Office. Вычислительный комплекс SCAD. — М.: Издательство АСВ, 2004. — 592 с.
3. Городецкий А.С., Евзеров И.Д. Компьютерные модели конструкций. — К.: Факт, 2005. — 344 с.