CADmaster

В этой статье мы хотели бы поделиться опытом применения программ SCAD Office в проектной практике инжинирингового центра «ГК «Электрощит"-ТМ-Самара». Центр эксплуатирует три рабочих места SCAD Office в следующих конфигурациях:

• два рабочих места размерностью 64  000 степеней свободы плюс необходимые в работе программы-сателлиты на сетевом ключе;
• одно рабочее место размерностью 392  000 степеней свободы плюс необходимые в работе программы-сателлиты на локальном ключе.

Представленное решение заслуживает внимания хотя бы потому, что правильный выбор конфигурации позволяет существенно экономить на программном обеспечении. Как будет показано далее, для фирмы, проектирующей металлоконструкции, в 95% случаев достаточно даже 32  000 неизвестных — поэтому советуем воспользоваться предложенной разработчиком гибкой системой поставки SCAD.

Мы отказались от старой практики, при которой часть специалистов, выполняющих рабочее проектирование, специализировалась исключительно на расчетах, и система SCAD стала таким же повседневным инструментом проектировщика, как чертежно-графический редактор. Специалист, занимающийся расчетами, выполняет разработку конструктивной схемы и формирует конструкторскую документацию. Это позволило повысить соответствие расчетной и конструктивной схем, а также исключить какие бы то ни было изменения конструктивной схемы без корректировки расчетной, и наоборот (такое рассогласование нередко случается при выполнении работ разными специалистами).

На рис. 1−9 представлены расчетные модели наиболее интересных объектов, запроектированных нами в течение года. Монтаж этих объектов либо продолжается, либо уже завершен.

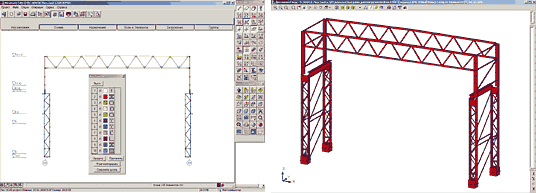
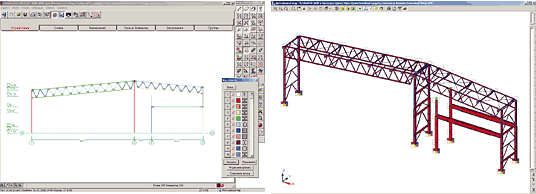
На рис. 1:

• слева — плоская модель поперечной рамы (325 степеней свободы);
• справа — расчетная модель связевого блока (1186 степеней свободы).

Порядок разработки и расчета подобных моделей подробно изложен в статье А. Маляренко и А. Теплых «Технологии построения расчетных моделей и анализа результатов в системе SCAD Office: модели металлокаркасов» [1]. Выполняя такие работы, необходимо учитывать расцентровки раскосов в узлах фермы, для чего модель с раскосами, сходящимися в узлах, после подбора сечений и их прорисовки перестраивается и повторно рассчитывается, что, впрочем, не очень сильно влияет на результаты расчета.

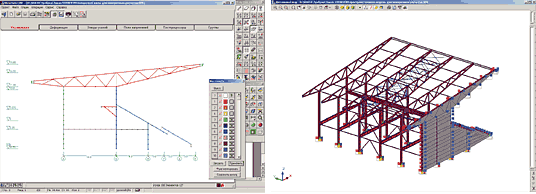
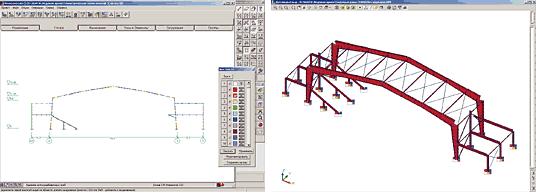
На рис. 2:

• слева — плоская модель поперечной рамы (610 степеней свободы);
• справа — пространственная расчетная модель деформационного блока, использованная для учета нагрузок от ветра в торец (4110 степеней свободы).

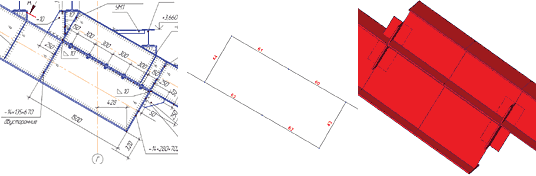
Одна из особенностей этой расчетной модели — моделирование узла жесткого стыка отправочных марок нижней и верхней частей главных балок трибуны (ее будущий облик показан на рис. 3). Конструкция узла и соответствующая расчетная схема, использованная для определения усилий, представлены на рис. 4. При расчете узла в запас прочности предполагается, что момент передается через пару сил, возникающую в элементах № 43 и 44. При таком подходе для расчета узла были использованы РСУ, полученные в расчетной модели для указанных элементов.

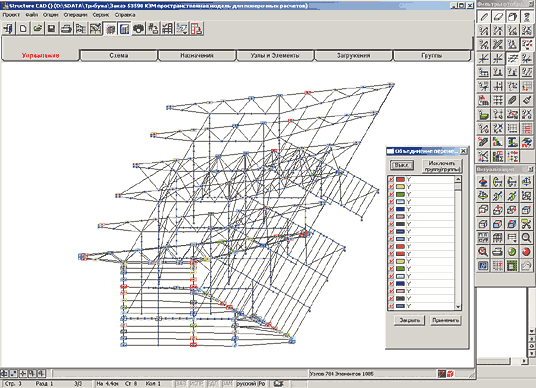
Расскажем о нескольких приемах, использованных нами при построении пространственной модели несущего каркаса трибуны.

На рис. 2 видно, что в пространственной расчетной модели отсутствуют прогоны покрытия и нет замыкающей распорки по связевому блоку покрытия со стороны оси А. Возможно, кажется непонятным назначение достаточно безобразных оболочечных элементов, ко всему прочему еще и закрепленных с торца по осям Z и X.

В этой модели рассчитывались связевые блоки и проверялась догрузка элементов поперечной рамы (фермы и колонны) от ветра в торец. На связевые блоки в расчетной модели нагрузка от ветра передана заданием объединения перемещений вдоль оси Y по узлам ферм (рис. 5). Чтобы в расчетной модели рассчитываемые распорки связевых блоков включились в силовую работу до и после связевого блока, по линии распорок заданы разные группы объединения перемещений. Прогоны покрытия рассчитывались отдельно и тратить время на их задание в пространственной модели не было никакого смысла, а роль крайней распорки играет удвоенное сечение прогона покрытия в этом месте. Оболочечные элементы с торца заданы исключительно для корректного распределения ветровой нагрузки на каркас. Толщина пластин — 1 мм (в данном случае это не очень существенно), жесткостные характеристики соответствуют стали. Пластины соединяются с каркасом только по оси Y путем объединения перемещений, а ветровая нагрузка, приложенная к пластинам, распределена на группу элементов (рис. 6) с возрастанием по оси Z — согласно эпюре изменения ветровых нагрузок, рассчитанной в программе ВеСТ. Для обеспечения геометрической неизменяемости расчетной модели во всех узлах пластин заданы закрепления по осям X и Z.

Перейдем к следующему проекту. На рис. 7:

• слева — расчетная модель поперечной рамы (751 степень свободы);
• справа — расчетная модель связевого блока (2812 степеней свободы).

Расчетная модель, показанная на этом рисунке, достаточно проста, а ее особенностью (как и в случае, представленном на рис. 1) является необходимость учета расцентровок раскосов в узлах ферм из гнутосварных замкнутых профилей. Кроме того, требуется учитывать изгибающий момент в поясах фермы.

Рис. 8 позволяет получить представление об архитектурном решении объекта.

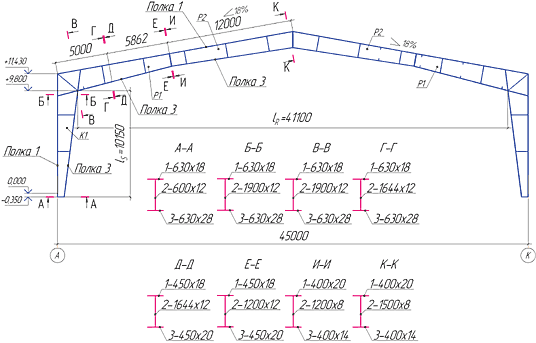
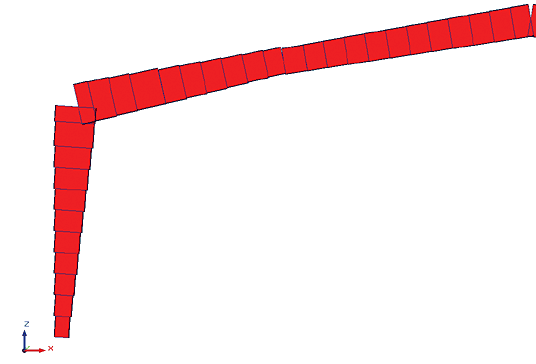
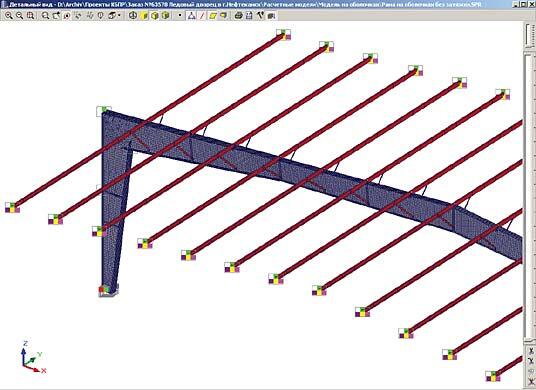
Следующий проект — ледовая арена в городе Нефтекамске.

На рис. 9:

• слева — расчетная модель поперечной рамы (643 степени свободы);
• справа — расчетная модель связевого блока (1510 степеней свободы).

Об особенностях моделей, представленных на этом рисунке, поговорим несколько подробнее:

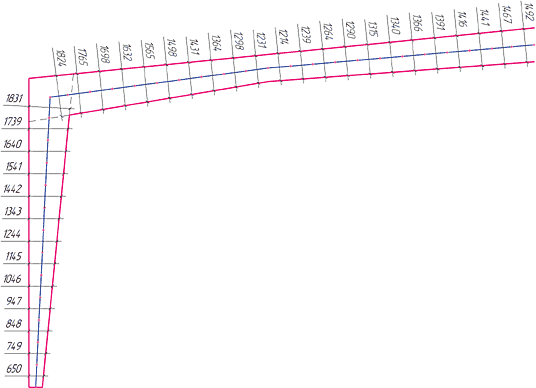
• В качестве расчетной модели рамы переменного сечения используется аппроксимация элементов рамы стержневыми элементами постоянного сечения. Как расчетная принимается ось, проходящая через центры тяжести двутавровых сечений элементов рамы. В процессе построения расчетной модели возникают сложности, которые достаточно эффективно решаются при вычерчивании рамы, расчетной оси и высот сечений в чертежно-графических системах. Средствами чертежно-графической системы выполняется и дробление стержней на конечные элементы, а в систему SCAD передается (через формат DXF или DWG) уже готовая геометрическая модель, в которой остается задать жесткости элементов, нагрузки и закрепления. Пример подготовки расчетной модели рамы переменного сечения представлен на рис. 11. Впрочем, у такого способа есть и недостаток: даже при наличии отработанной технологии на построение одной расчетной модели уходит порядка 8−12 часов работы опытного пользователя обеих систем. Учитывая, что для поиска приемлемого решения требуется просчитать 3−6 моделей, только построение геометрических моделей занимает до трех суток, а это не всегда приемлемо. На наш взгляд, в составе системы SCAD необходим генератор, разбивающий стержень по заданным сечениям в начале и в конце на заданное пользователем количество элементов постоянного сечения, аппроксимирующих стержень переменного сечения…

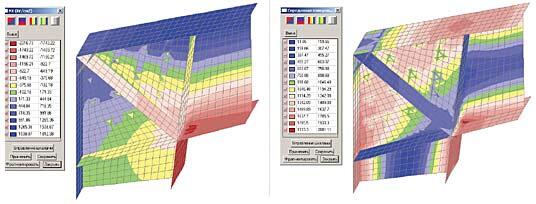
• Размеры элементов в зоне стыка ригеля и колонны не должны превышать расстояния от точки пересечения расчетных осей ригеля и колонны до продолжения поясов, изображенных на рис. 11 пунктирной линией. В процессе расчета эти элементы допускается исключить из проверок общей прочности и устойчивости, что подтверждается анализом напряженного состояния этой зоны на модели из оболочек (см. рис. 22).
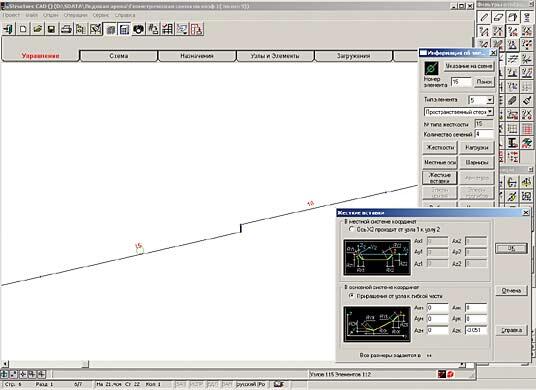
• В местах изменения толщины поясов расчетная ось, проходящая через центр тяжести, смещается. Для учета эксцентриситета здесь следует применять жесткую вставку, задаваемую в общей или местной системе координат, как это изображено на рис. 12.

• Поскольку высота каждого элемента задана в его середине, а расчетные сочетания усилий, на основе которых выполняются проверки в системе SCAD, выдаются как правило в трех точках, то на концах элементов, действительное сечение которых больше заданного в расчетной модели, возникает перегрузка на 3−5%. Для элементов, в которых из-за несоответствия размеров заданного и фактического концевого сечения элемента возникла перегрузка, требуется дополнительная проверка в программе КРИСТАЛЛ. Экспортировав в эту программу РСУ из системы SCAD, осуществить такую проверку будет нетрудно.
• При выполнении расчета устойчивости стенки возникают сложности, связанные с отнесением элементов к изгибаемым или сжато-изгибаемым, а также с отсутствием в СНиП II-23−81* правил расчета на устойчивость стенок сжато-изгибаемых двутавровых элементов переменного сечения. Для расчета стенок на устойчивость, а также для получения ответов на большинство остальных вопросов, касающихся расчета и проектирования рам переменного сечения, рекомендуем воспользоваться работой [2].
• Вертикальные связи по осям А/1 и Л и по покрытию выполнены из прутка диаметром 24 мм с преднапряжением. Отметим, что пока в сжатой от действия внешних нагрузок связи остается натяжение, она участвует в силовой работе связевого блока. При определении расчетных усилий в преднапряженных гибких связях необходимо включать в расчетную модель и растянутые, и сжатые элементы, а усилие натяжения связей должно приниматься по максимальному усилию в сжатой связи, полученному из расчетной модели с учетом коэффициента обеспечения заданного натяжения, принимаемого как >1. Подбор сечения и расчет остальных элементов гибких преднапряженных связей следует выполнять на суммарное усилие от предварительного натяжения и внешней нагрузки. Подробный анализ работы преднапряженных гибких связей и методика их расчета приведены в работе [2].

Более подробно остановимся на определении расчетной длины элементов рамы в плоскости действия нагрузок.

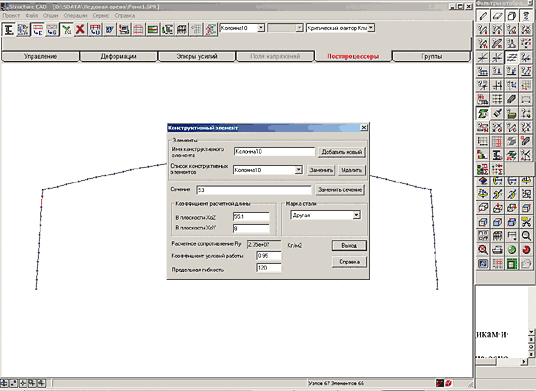
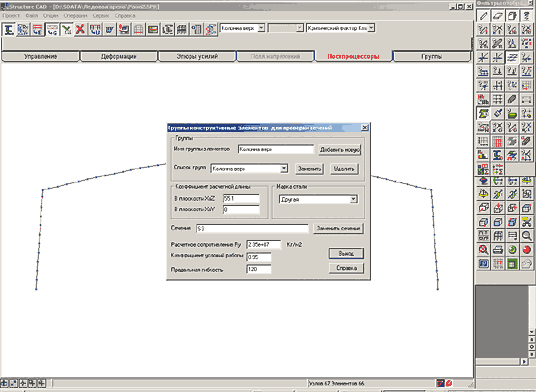
Существующие подходы изложены в [5] и [6] (с. 333 и 202 соответственно). В [2] этой теме посвящена целая глава. К сожалению, в упомянутых работах речь идет о расчетных длинах колонн, но при этом ни слова не сказано о расчетной длине ригеля, хотя ригель также работает как сжато-изгибаемый элемент. Основываясь на этих работах, мы определим расчетные длины колонны для рамы, расчетная модель которой представлена на рис. 9, а конструктивная схема с сечениями — на рис. 13, после чего представим методику определения расчетных длин стоек с помощью модуля устойчивости системы SCAD.

Согласно [5] и [6], коэффициент расчетной длины стержня переменного сечения определяется по формуле

ℓ_eƒ = μμ₁ℓ, где, согласно [6]:

• μ — коэффициент расчетной длины, характеризующий особенности работы стойки в системе рамы. Его назначают по общим правилам и принимают равным 2 при наличии шарнира в верхнем или нижнем узле и равным 1 при жестком сопряжении стойки с фундаментом;
• μ₁ — коэффициент, зависящий от отношения моментов инерции стойки в местах ее сопряжения с ригелем и фундаментом. Этот коэффициент можно определить по таблице 6.1 [5].

Для рассматриваемой однопролетной рамы (шарнирное сопряжение стоек колонн с фундаментами и жесткое сопряжение колонн с ригелями основных рам) значение μ = 2. Для определения μ₁ вычисляем отношение

Jmin

.

Jmax

, а для определения моментов инерции воспользуемся возможностями инженерного калькулятора КРИСТАЛЛ, позволяющего формировать отчет в формате RTF и тут же вставлять в полученный документ необходимые данные (рис. 13а).

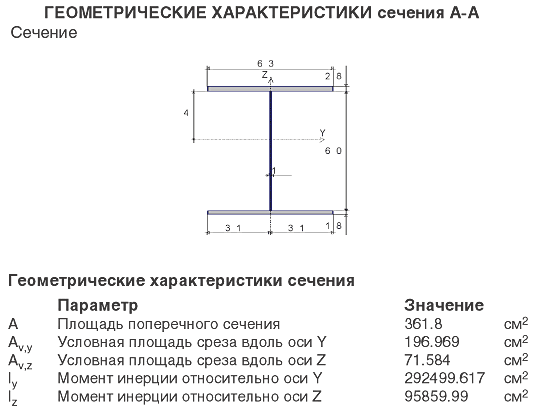
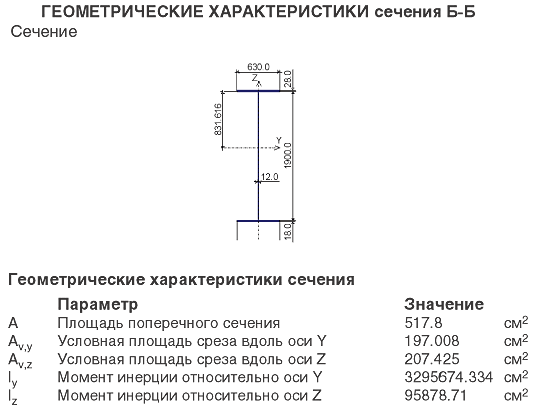
В верхнем сечении колонна имеет сечение и геометрические характеристики, приведенные на рис. 13б.

Следовательно, отношение

Jmin . Jmax

=

292500 . 3295674

= 0,089

, а определенное по таблице 6.1 [5] значение μ₁ = 1.66.

Коэффициент расчетной длины колонны основной рамы в плоскости изгиба, определенный по методике работы [5], будет равен

μ_eƒ = μμ₁ = 2×1,66 = 3,32.

Как будет показано ниже, коэффициент расчетной длины, определенный согласно [5] и [6], является заниженным: по-видимому, некорректна предложенная в работе [6] рекомендация принимать первый коэффициент равным 2.

Согласно [2], формула для определения расчетной длины крайней стойки переменного сечения имеет вид

μeƒ = 4

√ . 1+ 0.38kμ . n . √ . 1+3c

, где

• n =

  JRℓS . JSℓR

  ;

• ℓ_S и ℓ_R — длины стойки и ригеля, определяемые по осям до внутреннего края узла их пересечения;
• J_S и J_R — эквивалентные моменты инерции ригеля и стойки постоянного сечения;
• k_μ = 1 для однопролетных рам;

• c =

  Jmin . Jmax

  .

Для рамы на рис. 13:

• ℓ_S = 10,15 м;
• ℓ_R = 41,1 м;
• согласно [2], эквивалентный момент инерции для стойки переменного сечения определяется по равноустойчивой стойке постоянного сечения или принимается на расстоянии 0,333 от внутренней грани узла сопряжения ригеля и стойки. Соответственно J_S = 1964423 см⁴ определено для сечения на расстоянии 3,38 м от внутренней грани узла сопряжения стойки и ригеля;
• эквивалентное сечение ригеля находим по равенству углов поворота рассматриваемого ригеля переменного сечения и ригеля постоянного сечения, принимая в качестве расчетных схем шарнирно-опертый ригель рассматриваемой рамы переменного сечения и ригель постоянного сечения с приложенными к краям единичными моментами, как это изображено на рис. 14. Таким образом, J_R = 1386674 см⁴;

• n =

  JRℓS . JSℓR

  =

  1386674×10,15 . 1964423×41,1

  = 0,174;

• c =

  Jmin . Jmax

  =

  292500 . 3295674

  = 0,089;

• μeƒ = 4

  √ . 1+ 0.38kμ . n . √ . 1+3c

  = 4

  √ . 1+ 0.38 x 1 . 0,174 . √ . 1+3×0,089

  = 6,341.

Проверка устойчивости стойки переменного сечения выполняется согласно [2] по форме, аналогичной форме проверки устойчивости рамных конструкций переменного сечения, принятых в нормах проектирования США, — за исключением введенного автором [2] коэффициента запаса.

N ≤	Ncr, b . kb

, где N_{cr, b} — эйлерова критическая сила для стойки рамы, определенная с учетом поправочного коэффициента, а k_b — коэффициент запаса, полученный автором [2] путем деления критической силы для сжатого стержня, определенной по нормам [4], на критическую силу по формуле Эйлера.

Рассмотрим возможность определения расчетной длины колонны в плоскости рамы с применением модуля расчета на устойчивость системы SCAD и последующего расчета элементов рамы с использованием модуля расчета сечений металлопроката.

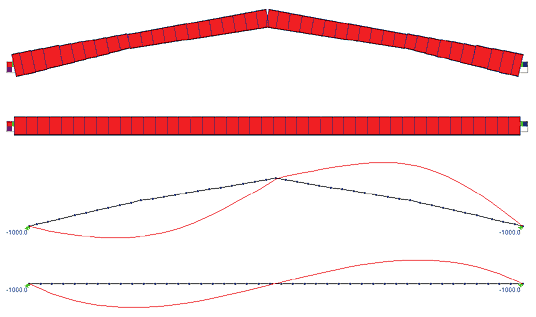
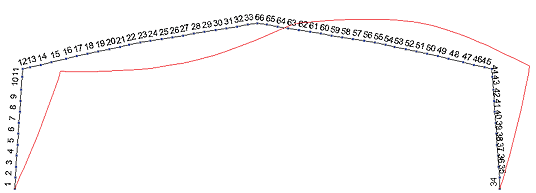
Поскольку для расчета рамы переменного сечения использована стержневая аппроксимация элементами постоянного сечения (рис. 15), то по аналогии со ступенчатыми стойками при расчетах по нормам [4] для каждого конечного элемента используется своя расчетная длина, полученная из расчета рамы на устойчивость.

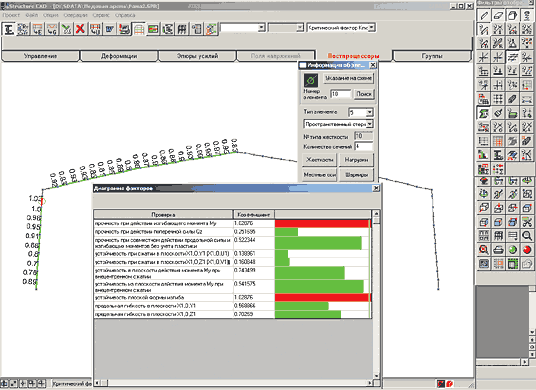
Форма потери устойчивости рамы в плоскости изгиба от всех вертикальных нагрузок представлена на рис. 16. Коэффициент запаса устойчивости, полученный в системе SCAD, равен 16,8.

В таблицах 1 и 2 представлены результаты расчета сводных длин для элементов 1−33 (левая часть рамы относительно конька).

Таблица 1

Результаты расчета свободных длин элементов стойки

№ эл.	1	2	3	4	5	6	7	8	9	10	11
LY	18,4	22,0	25,7	29,5	33,3	38,3	42,4	46,5	50,8	55,1	58,2

Таблица 2

Результаты расчета свободных длин элементов ригеля

№ эл.	13	14	15	16	17	18	19	20	21	22
LY	64,0	61,4	58,2	45,5	43,3	41,1	38,9	36,8	34,7	30,2
23	24	25	26	27	28	29	30	31	32	33
31,0	31,8	32,7	33,5	34,4	35,2	36,1	37,0	37,9	38,8	39,7

Для элемента № 10 свободная длина равна 55,1 м; соответственно коэффициент расчетной длины

μeƒ =

55,1 . 10,15

= 5,43

, что сопоставимо с коэффициентом расчетной длины, полученным по методике, изложенной в [2], — с погрешностью 14%.

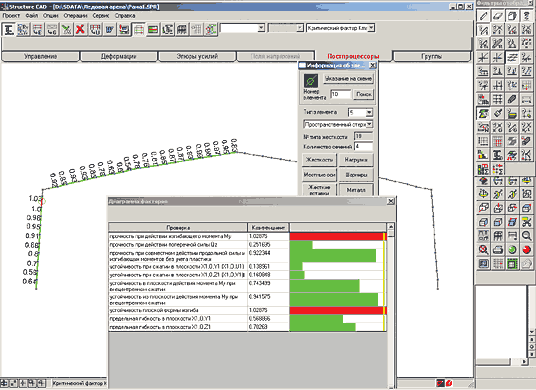
Далее при задании исходных данных в модуле системы SCAD можно рассматривать каждый конечный элемент системы как конструктивный со своим коэффициентом расчетной длины как в плоскости изгиба, так и из плоскости. При этом коэффициент расчетной длины каждого элемента определяется как отношение расчетной длины в плоскости или из плоскости изгиба к длине элемента. Пример задания исходных данных и результаты расчета модели, у которой каждый элемент задан как конструктивный, — на рис. 17 и 18. В то же время такой подход является достаточно трудоемким, поэтому можно использовать группы конструктивных элементов, разбивая колонну и ригель на две-три части и применяя для каждой группы максимальную расчетную длину по всем элементам, входящим в группу. В группы следует объединять только элементы с одинаковой длиной, тогда при определении расчетной длины в системе длина каждого конечного элемента, входящего в группу, умножается на коэффициент расчетной длины, заданный в исходных данных. На рис. 19 и 20 — пример задания исходных данных и результаты расчета при разбиении колонны и ригеля на две группы конструктивных элементов.

На рис. 18 и 20 видно, что элемент № 10 перегружен по прочности при действии изгибающего момента (п. 5.12 [4]) и по устойчивости плоской формы изгиба (п. 5.15 [4]), а коэффициенты использования по обоим критериям равны 1,02876. Одинаковые коэффициенты по прочности на действие момента и по устойчивости плоской формы изгиба следуют из равенства 1 коэффициента φ_b в формуле (34) [4], что подтверждается поверочным расчетом вручную. Проверка прочности на действие одного только момента М_y в данном случае является лишней, поскольку для моносимметричного двутавра с более развитым сжатым поясом сжимающая сила является разгружающей, чего нельзя сказать о симметричных двутаврах. Проверка по устойчивости плоской формы изгиба также не требуется: приведенный относительный эксцентриситет m_eƒ < 20 и расчет на устойчивость в том числе и по изгибно-крутильной форме следует выполнять как для сжато-изгибаемого элемента. Представленный подход определения расчетных длин стоек и ригеля достаточно хорошо увязывается с требованиями норм и логикой проектирования — в том числе и с точки зрения проверки по предельной гибкости. Следует также отметить, что устойчивость рамы в плоскости действия момента не является критичной — критичны прочность и устойчивость по изгибно-крутильной форме элементов при действии момента и сжимающей силы.

На наш взгляд, наиболее перспективной является следующая технология расчета рам переменного сечения, аналогичных рассмотренной:

1. Подбор параметров рамы на основе стержневой расчетной модели согласно методикам и алгоритмам, представленным в работе [2].
2. Поверочный расчет и окончательная оптимизация толщины полок и стенки рамы на основе модели из оболочек, при необходимости выполняемые в нелинейной постановке с учетом потери устойчивости стенки. На моделях из оболочек с гораздо большей наглядностью можно выполнить следующие расчеты:
   • поверочный расчет на прочность, основанный на анализе нормальных, касательных и эквивалентных напряжений;
   • расчет общей устойчивости рамы в плоскости изгиба;
   • расчет общей устойчивости рамы по изгибно-крутильной форме;
   • расчет местной устойчивости стенки и поясов;
   • расчет несущей способности рамы как единой нелинейной системы.

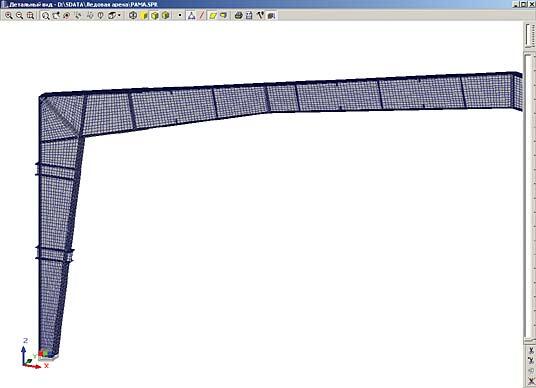
К сожалению, на момент написания этой статьи авторами отработаны только технология построения расчетной модели на оболочечных элементах в системе SCAD и поверочный расчет на прочность. Остальные позиции находятся на стадии исследований и отработки технологии. Пример расчетной модели рамы из оболочечных элементов представлен на рис. 21. На рис. 22 показаны изополя напряжений N_x и эквивалентных напряжений в узле стыка ригеля и колонны. Наиболее перспективной в плане расчета на устойчивость по изгибно-крутильной форме является модель, представленная на рис. 12, включающая распорки, прогоны и подкосы от прогонов к нижним поясам рам.

Следует отметить, что при кажущейся на первый взгляд сложности и трудоемкости построения расчетной модели отработанная технология построения такой модели требует тех же самых 8−12 часов рабочего времени. Размерность модели на оболочках (рис. 23) составляет 90  996 неизвестных.

На основании приведенных выше рассуждений и примеров систематизируем основные приемы построения расчетных моделей и выполнения расчетов рам переменного сечения с использованием системы SCAD.

1. В качестве расчетной модели используется аппроксимация элементов рамы стержневыми элементами постоянного сечения. Как расчетная принимается ось, проходящая через центры тяжести двутавровых сечений элементов рамы.
2. Геометрическую основу расчетной модели, включая разбивку на конечные элементы, удобнее всего выполнять в чертежно-графических системах, как это изображено на рис. 11. Более перспективным следует признать создание встроенных в систему или независимых генераторов расчетных моделей.
3. При разбивке расчетной оси конструктивных элементов на конечные элементы размеры последних лучше всего делать одинаковыми — это позволит более эффективно использовать возможности объединения конечных элементов в группы конструктивных элементов.
4. Сечение двутавра назначается по линии, перпендикулярной к расчетной оси и проходящей через середины конечных элементов.
5. Размеры элементов в зоне стыка ригеля и колонны не должны превышать расстояния от точки пересечения расчетных осей ригеля и колонны до продолжения поясов, изображенных на рис. 11 пунктирной линией. В процессе расчета эти элементы можно исключить из проверок общей прочности и устойчивости, что подтверждается расчетом этой зоны на модели из оболочек.
6. В местах изменения толщины поясов ось, проходящая через центр тяжести, смещается. Для учета эксцентриситета здесь следует применять жесткую вставку, задаваемую в общей или местной системе координат (см. рис. 12).
7. Расчетные длины элементов в плоскости изгиба рассчитываются в системе SCAD при расчете рамы на устойчивость и назначаются в модуле расчета сечений металлопроката либо для каждого конечного элемента, либо путем объединения элементов в группы конструктивных элементов с назначением расчетной длины, максимальной по всем элементам, входящим в группу.
8. Расчетные длины элементов из плоскости изгиба следует назначать согласно [4] или в соответствии с рекомендациями, приведенными в работе [2].
9. В случае применения моносимметричных двутавров проверка по прочности при действии момента не требуется. Проверка по устойчивости плоской формы изгиба также может оказаться лишней.
10. Поскольку элементы рамы переменного сечения аппроксимированы стержнями постоянного сечения и размеры на концах элементов отличаются от реальных, то при использовании модуля для проверки сечений металлопроката возможна перегрузка элементов расчетной схемы (для рассмотренной рамы и соответствующей расчетной модели перегрузка составляет порядка 4%). Если коэффициенты использования сечений при расчетах в системе SCAD превышают 1, возможен расчет реального сечения в программе КРИСТАЛЛ (РСУ импортируется из SCAD).
11. Параметры рамы, подобранные на стержневых расчетных моделях, оптимизируются на более точных оболочечных моделях. Это позволяет также выявить ошибки, допущенные при построении стержневой модели, и более наглядно представить работу конструкции.

Подводя некоторые общие итоги, отметим следующее:

• для всех зданий, основной несущей конструкцией которых является поперечная рама, подбор ее параметров выполняется с использованием плоских расчетных стержневых моделей. Такие модели достаточно просты для анализа и тестирования;
• для расчета связевых блоков и поверочных расчетов связевых рам используется пространственная стержневая модель, состоящая из рам, входящих в связевый блок;
• в исключительных случаях, когда применение плоских моделей невозможно или неэффективно, применяются пространственные стержневые модели;
• в исследовательских целях, а также для некоторых типов конструкций (например, рамных) необходимо применение моделей из оболочек, позволяющих рассчитывать конструкции более оптимально и точно — в том числе в нелинейной постановке с учетом эффектов, которые практически невозможно проанализировать на стержневых моделях. Для таких расчетных моделей конфигурация системы, обеспечивающая решение моделей с 64  000 неизвестных, будет уже недостаточной (размерность составляет 100−120 тыс. неизвестных).

Литература

1. А.А. Маляренко, А.В. Теплых. Технологии построения расчетных моделей и анализа результатов в системе SCAD Office: модели металлокаркасов. — CADmaster, № 4/2004, с. 93−97.
2. В.В.Катюшин. Здания с каркасами из стальных рам переменного сечения (расчет, проектирование, строительство). — М., Стройиздат, 2005. — 656 с.: ил.
3. А.В. Перельмутер, В.И. Сливкер. Расчетные модели сооружений и возможность их анализа. — Киев, Сталь, 2002. -600 с.: ил.
4. СНиП II-23−81*. Стальные конструкции/Госстрой России. — М.: ГУП ЦПП, 2000. — 96 с.
5. В.В. Горев, Б.Ю. Уваров, В.В. Филиппов и др. Металлические конструкции. В 3 т. Т. 1. Элементы конструкций. Учеб. для строит. вузов. — 3-е изд., стер. — М., Высшая школа, 2004. — 551 с.: ил.
6. В.В. Горев, Б.Ю. Уваров, Б.И. Белый. Металлические конструкции. В 3 т. Т. 2. Конструкции зданий. Учеб. для строит. вузов. — 3-е изд., стер. — М.: Высшая школа, 2004. — 551 с.: ил.
7. В.С. Карпиловский, Э.З. Крискунов, А.А. Маляренко, А.В. Перельмутер, М.А. Перельмутер. Вычислительный комплекс SCAD. — М., АСВ, 2004. — 529 с.