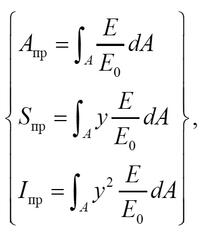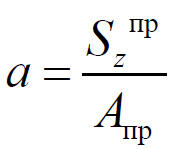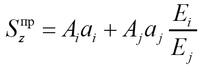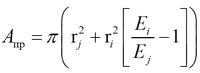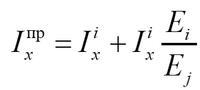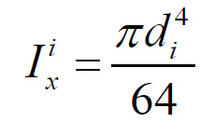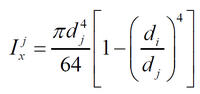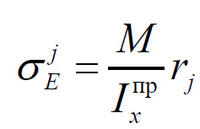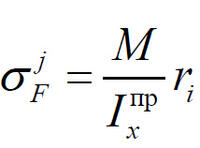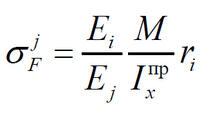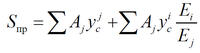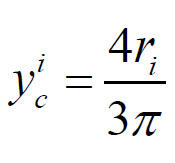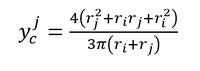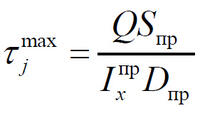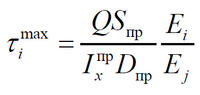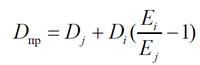CADmaster

При изготовлении прокатных валков разнородной упругости (состоящих из различных материалов рабочего слоя и центральной части валка) достаточно остро стоит вопрос получения здорового тела изделия в процессе его термообработки [1]. Следует отметить, что зачастую нарушение сплошности тела валка происходит по границе сопряжения рабочего слоя с материалом сердцевины — это связано с возникающими термическими, фазовыми напряжениями, а также с напряжениями от изгиба, возникающего при двух- или четырехточечном креплении валка при его термообработке [2]. Рассмотрим вопрос о возникновении напряженного состояния по сечению валка вследствие деформаций изгиба.

При расчете на изгиб бруса разнородной упругости все его геометрические характеристики приводятся к одному материалу [3]. При вычислении геометрических характеристик величина площади поперечного сечения, принадлежащей каждому материалу, умножается на коэффициент, равный соотношению модуля упругости данного материала и модуля упругости приводимого материала (обычно того, площадь которого больше) [4].

Таким образом, выражения геометрических характеристик будут иметь вид:

где А_пр, S_пр, I_пр — геометрические характеристики приведенного сечения: площадь, статический момент, момент инерции соответственно;

Е, Е₀ — модули продольной упругости соответствующей элементарной площадки dA и приводимого материала соответственно.

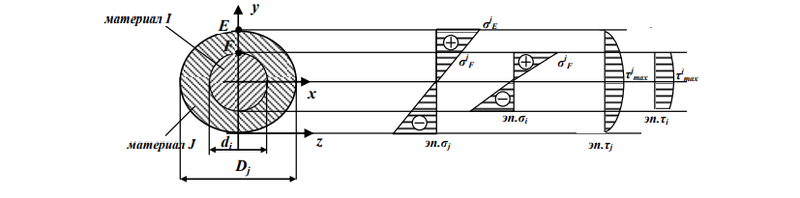
В работе мы будем рассматривать два жестко сопряженных элемента круглого и кольцевого сечения из различных материалов j, i (рис. 1).

Определим центр тяжести приведенного сечения по формуле [5]

,

(1)

где A_пр — приведенная площадь сечения, см²;

S_z^пр — статический момент приведенного сечения, см³.

Статический момент приведенного сечения определяется как [5]

,

(2)

где A_i, A_j — площади i-го и j-го материала, см²;

а_i, а_j — расстояния от оси z до центра тяжести фигур из материалов i, j, см;

E_i, E_j — модули продольной упругости материалов i, j, МПа.

Рис. 1. Схема напряженного состояния биметаллического валка при изгибе

Приведенную площадь сечения определим как [5]

,

(3)

где r_i, r_j — радиусы элементов из i-го и j-го материала, см.

Через найденное расстояние а проведем нейтральную ось х.

Определим приведенный осевой момент инерции относительно нейтральной оси х как [5]

,

(4)

где I_x^пр — приведенный осевой момент инерции относительно нейтральной оси х, см⁴;

I_xⁱ, I_x^j — моменты инерции сечений из материалов i, j, см⁴.

;

(5)

.

(6)

Возникающие на стыке материалов i и j нормальные напряжения в точке F, а также максимальные нормальные в точке Е и касательные (см. рис. 1) определим по формулам:

;

(7)

;

(8)

.

(9)

Для определения касательных напряжений найдем приведенный статический момент [5]:

,

(10)

где y_cⁱ, y_c^j — расстояние от нейтральной оси х до центра тяжести фигур из материалов i, j, см.

Для полукольца и полукруга y_cⁱ, y_cⁱ определяются как

;

(11)

(12)

Тогда, используя уравнение Журавского [5], максимальные касательные напряжения определим как

;

(13)

,

(14)

где D_пр — длина волокна сечения, по которому определяются касательные напряжения, см.

.

(15)

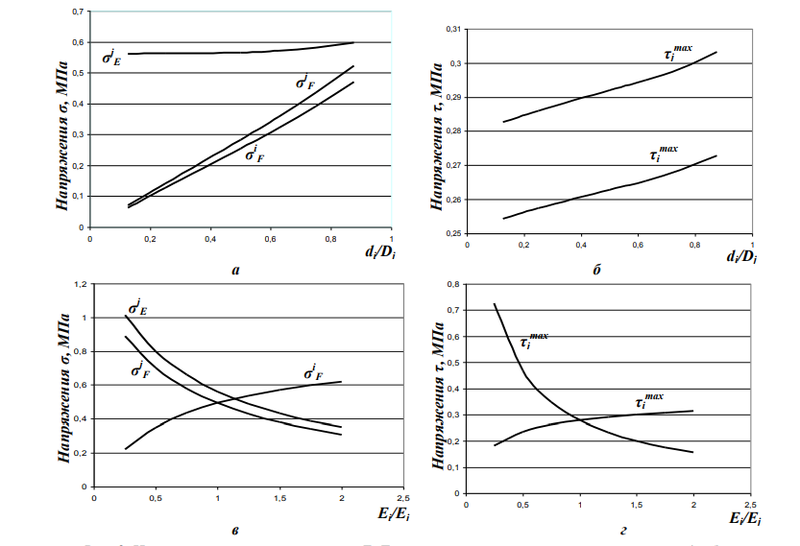
Применим выражения 7−9, 13, 14 для расчета напряженного состояния бочки двуслойного прокатного валка диаметром 820 мм и длиной 2200 мм, толщина стенки бандажа 50 мм, при двухконтактной опоре валка в процессе его термообработки. При весе бочки валка 221кН максимальный момент, возникающий в сечении, будет равен 6077,5 кНсм, максимальное поперечное усилие 110,5 кН. Определим возникающее напряженное состояние в характерных точках Е, А (см. рис. 1) при изгибе валка. Рассмотрим изменения, происходящие при изменении соотношения диаметров рабочего слоя валка и основного материала (рис. 2). При расчете зависимостей (см. рис. 2а, б) модуль продольной упругости принимался для материала j — 2·10⁵ МПа, i — 1,8·10⁵ МПа. При расчете зависимостей (см. рис. 2в, г) диаметры принимались равными D_j = 820 мм, d_i = 720 мм.

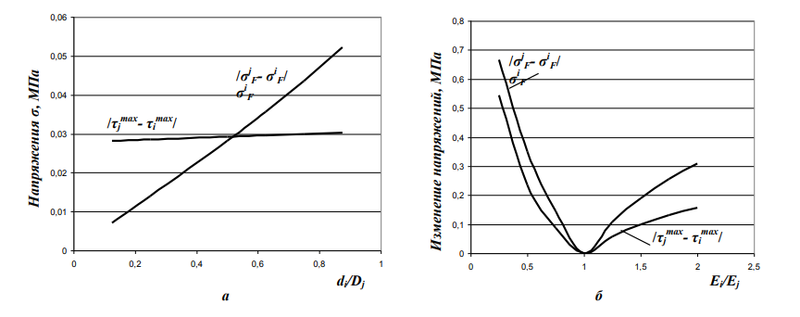
Как видно из рис. 2, уменьшение стенки бандажа (материал j) приводит к росту напряженного состояния в исследуемых характерных точках E, F. Это связано прежде всего с разными механическими характеристиками двух материалов, выраженных в данном случае модулями продольной упругости. Максимальные нормальные напряжения возникают в точке Е, что согласуется с уравнением Навье, определяющим распределение нормальных напряжений при изгибе стержня. Вместе с тем следует отметить, что с уменьшением толщины стенки бандажа растет разность напряжений на границе двух материалов (рис. 3) и, как следствие, увеличивается вероятность нарушения сплошности валка в процессе его термообработки по границе свариваемости, зачастую имеющей более низкие прочностные характеристики по сравнению с механическими свойствами свариваемых материалов. Аналогичную картину мы видим при исследовании максимальных касательных напряжений (см. рис. 2б).

Рост касательных напряжений при увеличении внутреннего диаметра бандажа также связан с различными модулями продольной упругости свариваемых материалов, однако разность касательных напряжений двух материалов в точке сопряжения практически постоянна (см. рис. 3а).

Рис. 2. Изменение напряжений в точках Е, F в зависимости от соотношения диаметров (а, б) и модулей упругости (в, г) бандажа и основного слоя прокатного валка

Влияние материалов рабочего слоя и основы на возникающие напряжения выразили через соотношение модулей упругости Ei/Ej. Полученное решение представлено на рис. 2в, г. Как видно из графика, изменение механических свойств материала значительным образом сказывается на разности как нормальных (рис. 2), так и касательных (рис. 2г) напряжений на границе свариваемости «рабочий слой — сердцевина». Это особенно хорошо заметно на рис. 3б, где показана разность по модулю напряжений рабочего и основного слоя, взятая в точке свариваемости F. Исходя из графиков, видно, что значительное изменение свойств материала приводит к росту абсолютных отклонений как касательных, так и нормальных напряжений, что в соответствии с законом Гука говорит о значительном различии возникающих деформаций. Следовательно, чем больше отклонение в модулях продольной упругости материала бандажа и основы, тем выше вероятность расслоения по границе свариваемости.

Рис. 3. Абсолютное изменение напряжений на границе материалов в зависимости от соотношения диаметров (а) и модулей упругости (б) бандажа и основного слоя прокатного валка

Таким образом, в результате проведенной работы адаптирован математический аппарат, обеспечивающий определение напряженного состояния по сечению двуслойного прокатного валка при изгибе.

Выявлено, что уменьшение стенки рабочего слоя прокатного валка приводит к росту напряженного состояния как по сечению, так и на границе свариваемости бандажа и сердцевины при изгибе в процессе термообработки изделия.

Установлено, что чем больше отклонение в значениях модуля продольной упругости материалов рабочего слоя и основы, тем больше возникающие напряжения по границе свариваемости материалов, а также по сечению в целом.

Литература

1. Савинов А.С., Тубольцева А.С. Расчет напряжений в углеродистых сталях при высоких температурах / Современные технологии в машиностроении: сборник XV Международной научно-технической конференции. — Пенза: Приволжский дом знаний, 2011. С. 38−40.
2. Савинов А.С., Прогнозирование напряжений в толстостенных отливках при деформациях в температурном интервале хрупкости / Савинов А.С., Тубольцева А.С., Зарицкий Б.Б. / В сборнике: Актуальные вопросы в научной работе и образовательной деятельности. / Сборник научных трудов по материалам Международной научно-практической конференции: в 10 томах. 2015. С. 128−130.
3. Савинов А.С. Прогнозирование механических свойств стали / Савинов А.С., Зарицкий Б.Б. / В сборнике: Итоги научных исследований. Сборник статей Международной научно-практической конференции. 2015. С. 22−26.
4. Третьяков А.В., Трофимов Г.К., Гурьянова Н.К. Механические свойства сталей и сплавов при пластическом деформировании. — М.: Машиностроение, 1971. 63 с.
5. Феодосьев В.И. Сопротивление материалов. — Учебное пособие. 17-е изд. — М: МГТУ им. Н.Э. Баумана, 2018. — 542 с. — ISBN 978−5−7038−4819−7. — Текст: электронный // Лань: электронно-библиотечная система. — URL: https://e.lanbook.com/book/106484 (дата обращения: 10.11.2020). — Режим доступа: для авториз. пользователей.

Скачать статью в формате PDF — 1.26 Мбайт