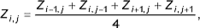CADmaster

Мягкие оболочки (МО) широко применяются как в сезонных, так и в капитальных сооружениях. Наиболее распространенные в малых архитектурных формах (навесы, знаковые сооружения), они получили известность благодаря использованию в большепролетных сооружениях — выставочных комплексах в Осло, Осаке (Экспо`70, Япония), Бордо (Франция) и Брисбене (Экспо`88, Австралия), летнем театре в Каннах, международном аэропорту Джидда в Саудовской Аравии…

Легкость, выразительность, динамичность архитектурного образа объектов достигается за счет специфичных свойств основного конструктивного элемента — механически растянутой (напряженной) безизгибной мягкой оболочки. Устойчивость геометрии обеспечивает форма поверхности отрицательной гауссовой кривизны (ОГК). Такие оболочки называются тентовыми или, сокращенно, ТО. Форму поверхности обусловливают геометрия опорного контура, условия преднапряжения и крепления к несущим конструкциям покрытия — иначе говоря, условия на контуре. Даже незначительное изменение этих условий ведет к формированию новой формы поверхности — с другими значениями площади покрытия и внутреннего объема, иными условиями механической работы. Отсюда богатый выбор форм, оригинальность сооружений, но и большая сложность проектных работ, связанных с определением исходной геометрии поверхности.

Исходная форма тентовой оболочки, определяющая архитектурный облик объекта, устанавливается на этапе эскизного проектирования. Качественный архитектурный, функциональный и конструктивный анализ требует достаточно точного, детального описания и графического отображения топологии поверхности. Исследования в области формообразования тентовых оболочек ведут многие отечественные научно-исследовательские и проектные институты, вузы (ЛенЗНИИЭП, ЦНИИСК, НИИЖБ, КиевЗНИИЭП, МНИИТЭП, Моспроект, Укрпроектстальконструкция, МИСИ, КГАСА). Для определения топологии поверхности, как правило, используют методы физического моделирования на основе жидких пленок и эластичных материалов, а также графоаналитические и численные методы.

Метод физического моделирования весьма нагляден и позволяет достаточно точно моделировать поверхность, форма которой приближена к минимальной. При этом он очень трудоемок, зависит от масштаба модели и физико-механических свойств ее материала.

Аналитический метод обеспечивает высокую точность построения описанных формулами поверхностей и параметрическое управление геометрией, но ограничен невозможностью моделирования поверхности на опорном контуре произвольной геометрией и небольшим набором аналитически описанных поверхностей, применяемых для моделирования тентовой оболочки. Используя численные методы, удается моделировать различные условия на контуре, строить поверхность любой сложности (если представлены исходные данные, в том числе начальная геометрия), а также максимально автоматизировать весь процесс проектирования — от определения исходной геометрии поверхности до прочностного расчета и раскроя.

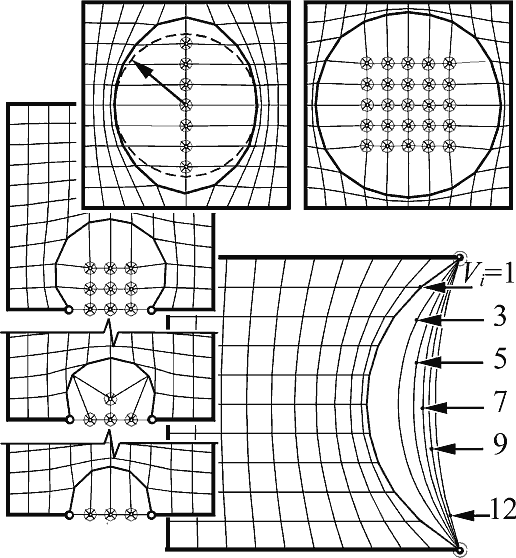
К сожалению, в большинстве своем численные методы отличаются повышенной трудоемкостью и громоздкостью расчета, что исключает оперативное управление процессом формообразования. Обычно к ним обращаются при расчете и уточнении конечного варианта тентовой оболочки, а для получения расчетной схемы, исходной формы поверхности применяют более простые, но высокопроизводительные методы. Именно один из таких численных методов стал исходным при разработке метода интерактивного моделирования тентовых оболочек, в основу которого положена идея поузловой трансформации изначально плоской сеточной модели оболочки, закрепленной на неизменяемом опорном контуре. В ходе анализа пересечений проекции опорного контура и рядов сети определяются внешние, внутренние и контурные узлы. Для последних, исходя из геометрии опорного контура, вычисляется ордината Z. Далее последовательно уточняются ординаты внутренних, незакрепленных узлов сети. Вычисления производятся по формуле:

Формула, по которой производятся вычисления

где i, j — номер узла в матрице сети.

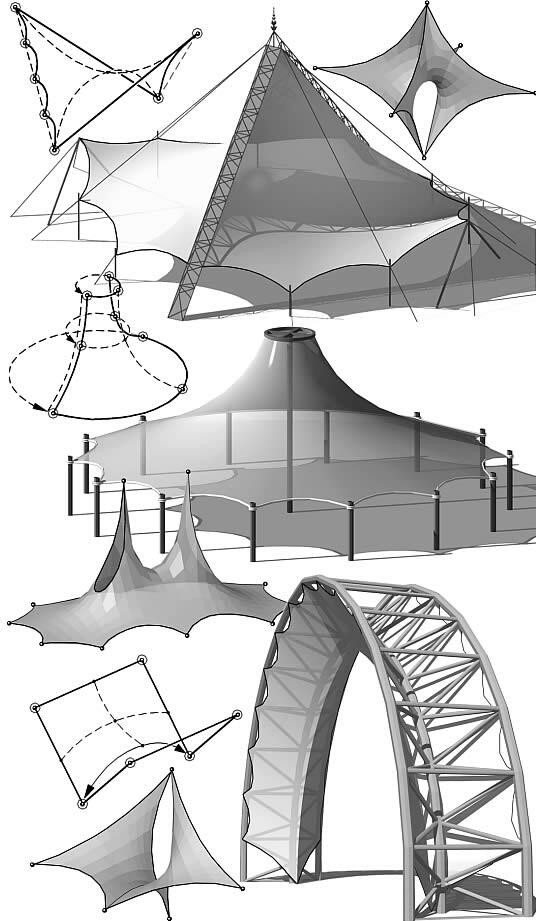
То есть определяется среднее арифметическое от координат ближайших узлов сети. Этот процесс повторяется до тех пор, пока все координаты узлов предыдущего и последующего приближения не будут отличаться на заранее определенную величину, характеризующую точность, степень приближения сети к искомой форме поверхности. Впрочем, полученная таким методом поверхность недостаточно точно отражает форму тентовой оболочки. Связано это с тем, что пропорции сторон ячеек сети на плоскости проекции и на поверхности тентовой оболочки не совпадают, поэтому на «сложном» опорном контуре, крутых участках поверхности (к плоскости проекции) точность построения снижается. То же происходит при переходе к цилиндрической или сферической системам координат (рис. 1), к которым прибегают, если проекция контура и внутренних участков поверхности на плоскость невозможна без взаимного наложения и пересечения (рис. 2). Кроме того, исходный метод не позволяет варьировать форму поверхности без изменения геометрии контура. Поэтому нами проведены исследования, целью которых было определение основных параметров формообразования ТО и их учет при расчете поверхности.

Рис. 1

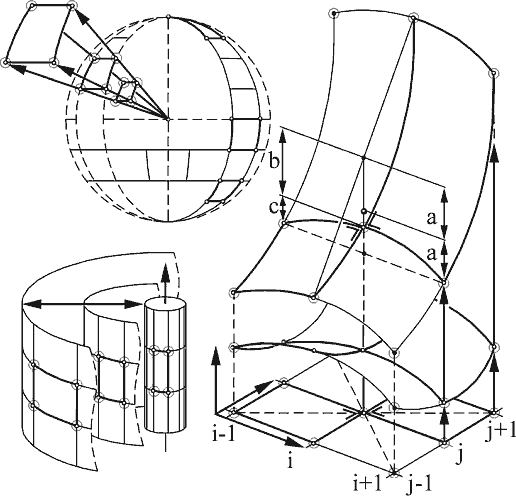
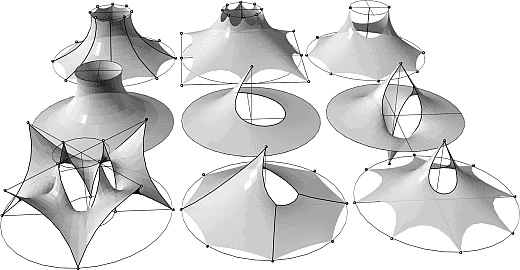
Как уже сказано, поверхность тентовой оболочки должна обладать отрицательной гауссовой кривизной (она обеспечивает устойчивость формы в процессе эксплуатации), для чего требуется закрепление мягкой оболочки минимум в четырех точках, не лежащих в одной плоскости. Если все точки крепления мягкой оболочки расположены на внешнем контуре — образуется «седловидная» форма поверхности. Ее аналогом может служить поверхность гиперболического параболоида (рис. 2, 3). «Воронкообразная» форма образуется при закреплении внутренних точек, выведенных из плоскости поверхности. Аналоги этой формы — к примеру поверхности вращения параболы, гиперболы или цепной линии — позволяют рассматривать «воронкообразную» форму и как частный случай замкнутой «седловидной» (рис. 3). Разнообразие форм достигается изменением геометрии опорного контура и характера предварительного напряжения. При этом мягкая оболочка может закрепляться по всей длине контура или в отдельных узлах: в первом случае мы имеем жесткий контур, геометрия которого совпадает с опорным контуром, во втором — гибкий контур. Форма гибкого контура зависит от раскроя поверхности (рис. 4) и характеризуется стрелой подъема или отношением его длины к расстоянию между узлами крепления. Использование гибкого контура, варьирование его длины позволяет получить эффектные, выразительные формы поверхности.

Рис. 2

При перекрытии больших пролетов тентовые оболочки, как правило, подкрепляются (стабилизируются) тросами. На внутренних участках это может привести к нарушению гладкой формы поверхности и образованию на ней граней. Частным случаем их проявления можно считать «складчатые» поверхности. Линии граней и форма складок позволяют ярче выразить динамику поверхности. Складки представляют собой смежные участки гиперболической формы с общим гибким контуром — на этом основании их можно отнести и к разновидности составных конструкций. Независимо от того, каким образом сформирована поверхность, желательно, чтобы ее форма была приближена к минимальной. Средняя кривизна такой поверхности, в любой точке равная нулю, позволяет обеспечить экономию материала и оптимальные прочностные характеристики. Аналогом минимальной поверхности может служить мыльная пленка, «натянутая» на рассматриваемый контур. На практике при решении функциональных, конструктивных и архитектурных задач от этой формы нередко приходится отклоняться, но даже и в этом случае минимальная поверхность необходима в качестве исходной формы, относительно которой устанавливаются параметры изменения геометрии тентовой оболочки.

Рис. 3

Анализ форм, условий формообразования тентовых оболочек позволил определить основные направления развития исходного метода. Это построение поверхности, приближенной к минимальной, и моделирование различных условий на контуре, включающие изменение кривизны поверхностей, моделирование гибкого контура и стабилизирующих вант. В процессе анализа исходного метода был решен ряд частных задач, связанных с определением оптимальной ориентации плоскости проекции и плотности сети относительно опорного контура, а также рассмотрен порядок перебора узлов. Это позволило на 50−80% по сравнению со стандартными решениями ускорить расчет формы. Для повышения точности расчета поверхности в условиях искажения пропорций ячеек сети и для моделирования различных условий на контуре в основную формулу были введены коэффициент M и параметры K и V.

Рис. 4

Коэффициент M учитывает искажение геометрии ячеек сети. При построении поверхности геометрия сети изменяется, поэтому необходимо постоянное обновление значения коэффициента. Его использование позволило уменьшить плотность сети, разместить «контурные» узлы по линии крепления мягкой оболочки и моделировать гибкий контур (рис. 5). Что же касается искажений геометрии ячеек сети, то в ходе расчета они равномерно распределяются по всей поверхности. Чтобы обеспечить эти условия, требуется определять все три координаты узлов сети — X, Y и Z. Использование коэффициента M позволяет обеспечить приемлемую точность построения и сократить время расчета, за которое достигается необходимый уровень приближения к искомой форме поверхности.

Рис. 5

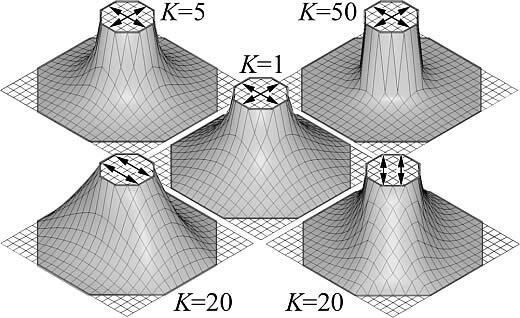
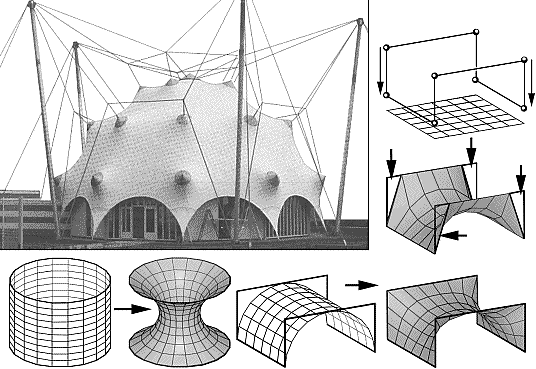
Для построения поверхности, отличной от минимальной, используется параметр K ]0;+ [ - он отвечает за изменение кривизны поверхности и отражает отношение нормальных усилий или радиусов главных кривизн в каждой ее точке (ρ_гл1 K = -ρ_гл2). Значение параметра постоянно, но при расчете его присвоение узлам требуется контролировать. Это связано с изменением ориентации линий главных кривизны на разных участках поверхности или в одной и той же точке по ходу формообразования тентовой оболочки. Закрепление параметра за одним из направлений относительно рядов сети позволяет моделировать натяжение мягкой оболочки в том же направлении (рис. 6, 7).

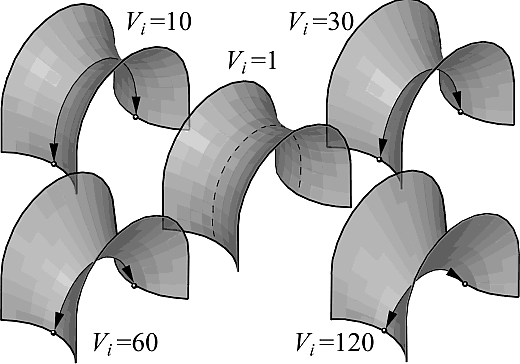
Для моделирования внутренних стабилизирующих вант используется параметр V_i ]1;+ [. Так же, как и параметр K, он отражает отношение радиусов кривизны поверхности, но изменяет кривизну поверхности только по линии прохождения троса. Значение параметра постоянно, присваивается индивидуально для каждого гибкого контура или стабилизирующей ванты. Изменение значений параметра позволяет регулировать форму, кривизну, длину ванты, проходящей через рассматриваемый узел (рис. 6, 7). Так, при V_i + длина троса приближается к расстоянию между узлами крепления. Поскольку форма и длина кривой зависят от исходной геометрии поверхности, плотности и ориентации сети, аппроксимирующей поверхность, для получения необходимой геометрии поверхности приходится подбирать значения параметра. Поэтому для построения поверхности с фиксированной длиной внутренней стабилизирующей ванты или гибкого контура разработан алгоритм: он позволяет контролировать длину и подгонять значение параметра по ходу построения поверхности. Предварительно определяется максимальная длина ванты — это делается на основе анализа геометрии исходной формы поверхности, полученной при V_i = 1. Увеличение длины сверх установленной возможно только для гибкого контура за счет раскроя поверхности, то есть изменения исходной геометрии сети.

Рис. 6

Рис. 7

Определяя значения параметров, следует учитывать, что на этапе эскизного проектирования они служат только для управления геометрией оболочки. При построении поверхности, приближенной к минимальной, значения параметров K и V принимают равными единице. В этом случае требуется вычисление только коэффициента M. Дополнительные расчеты компенсируются повышением точности построения и, как следствие, более быстрым определением искомой формы поверхности. Значения параметров подбирают исходя из геометрии минимальной поверхности. Визуальный контроль ввода исходных данных и изменения геометрии тентовой оболочки обеспечивают интерактивный режим проектирования. Это достигается использованием AutoCAD. В качестве графической оболочки мы использовали программу AutoCAD 13−2000. С помощью встроенного языка программирования (LISP) был получен доступ к командам и графической базе данных элементов. Разработанные в ходе исследований программы вычисления и анализа поверхности тентовой оболочки были объединены в приложение к AutoCAD, включившее в себя подготовку исходных данных, сортировку узлов сети, ввод формообразующих параметров, расчет поверхности, анализ геометрии и другие модули.

Рис. 8

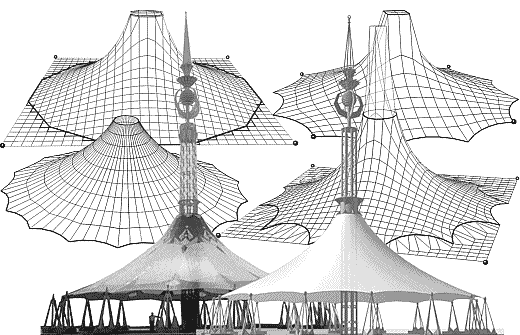
В связи с тем, что LISP — это язык-интерпретатор, достаточно медленно (в том числе и после компиляции в «Visual LISP») обрабатывающий данные, основные вычисления были переведены во внешний ARX-модуль. Интерактивный режим управления геометрией ТО в среде AutoCAD осуществляется за счет графических методов ввода данных (определения исходной сети, опорного контура, вант предварительного напряжения). Программа обладает повышенной устойчивостью и независимостью модулей подготовки исходных данных, расчета и анализа формы поверхности: все изменения, установки и параметры сохраняются в базе данных графического примитива «СЕТЬ», которая используется для моделирования поверхности тентовой оболочки. Кроме того, устанавливается режим автоматического сохранения по ходу вычисления формы. Палитру вариантов можно получить копированием сети и редактированием ее базы данных (рис. 7). Обновление координат (узла, ряда, сети) в графической базе данных сети помогает отслеживать на экране процесс формообразования поверхности. До завершения расчета поверхности можно вносить изменения в условия формообразования. Большой набор программ и приложений к AutoCAD позволяет объединить в одном рисунке различные виды проектных работ — от расчета конструкций до раскроя поверхности. Средства AutoCAD обеспечивают не только ввод, редактирование, контроль и анализ графической информации, но и ее вывод в виде чертежей и разрезов, аксонометрических и перспективных видовых кадров, включая фотореалистические изображения.

Рис. 9

Создание инструмента интерактивного моделирования исходной геометрии тентовой оболочки производилось на базе лицензионных программных продуктов авторизированного учебного центра Autodesk «Радиус» при ЦНИТАС и кафедры САПР КГАСА. В порядке экспериментальной проверки метода (а также с целью внедрения технологии) для персональной творческой мастерской архитектора В.А. Сладкова были разработаны эскизные проекты, рассчитаны формы и получен раскрой ряда покрытий ТО над трибунами, сценами, выставочными и торговыми комплексами в Казани, Набережных Челнах, Нижнекамске. Среди реализованных объектов — знаковое сооружение Майдана в Нижнекамске (рис. 5, 8). В ходе работ над объектом были испробованы различные методы построения исходной поверхности ТО и выполнен эскизный проект сооружения (рис. 8). Построенные объекты с ТО успешно эксплуатируются в зимних условиях Татарстана.

Скачать статью в формате PDF — 390.2 Кбайт