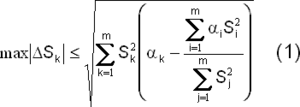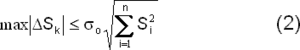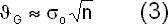CADmaster

Введение

Авторы этой публикации уже не первый десяток лет работают в области создания и применения программных систем для выполнения статических и динамических расчетов строительных конструкций. И за это время на собственном опыте убедились в наличии явно выраженной тенденции: используемые расчетные схемы постоянно усложняются, а их размерность увеличивается. Разработчики твердо знают, что любые их достижения в наращивании количественных возможностей программ быстро перекрываются пользователями. А пользователи считают большим достижением возможность проведения расчета целого здания, да еще совместно с основанием, как единой системы, и тяготеют к все большей детализации, учету большого числа подробностей. Является ли использование усложненных и детализированных расчетных моделей благом? Есть ли другие пути получения качественных результатов? Ответить на эти и смежные вопросы попробуем, основываясь главным образом на рассмотрении возможностей и особенностей вычислительного комплекса Structure CAD (SCAD) — разработки достаточно типичной и позволяющей проанализировать современный подход к проблеме.

Два типа задач большой размерности

Расчетные задачи большой размерности совершенно естественно возникают при анализе трехмерных проблем механики сплошной среды в конечно-элементной постановке. При характерном числе шагов конечно-элементной сетки, равном m, количество неизвестных перемещений пропорционально 3m³, что быстро наращивает размер задачи до десятков тысяч неизвестных даже в случае областей, не слишком отличающихся от канонических. Именно такие пространственные задачи порождают естественный спрос на программы большой мощности, для удовлетворения которого разработчики непрерывно наращивают мощность программ. Но затем эти программные продукты используются и при решении задач расчета стержневых несущих каркасов; у расчетчика возникает соблазн применить, не слишком мудрствуя, подробную расчетную схему такого каркаса, включающую в себя десятки тысяч упругих элементов и узлов.

Казалось бы, никакой разницы между этими ситуациями нет. Однако это не так. Задача механики сплошной среды для своего описания требует только аккуратного задания геометрии тела, а характеристики материала задаются несколькими параметрами. Для сложного стержневого каркаса массив исходных параметров, характеризующих задачу, весьма велик и разнороден. Учитывая, что большинство таких параметров по сути являются случайными величинами, для которых расчетчик задает лишь некоторую возможную реализацию значений, с увеличением числа задаваемых параметров возрастает степень не-определенности расчетной модели в целом.

Так, для шарнирно-стержневых систем, содержащих m элементов с усилиями S_k (k=1, …, m), была получена оценка максимально возможного отклонения этих усилий, возникающего при вариации площадей поперечного сечения

Оценка максимально возможного отклонения усилий, возникающих при вариации площадей поперечного сечения

где: через α_i обозначено относительное изменение площади поперечного сечения фермы (α_i = ΔA_i/A _i). Если предполагать, что величины α_i являются случайными, статистически независимыми и распределенными по нормальному закону с нулевым средним и одинаковым для всех стандартом σ_о, то там же установлена оценка

Оценка максимально возможного отклонения усилий, при случайных статистических отклонениях

где n — степень статической неопределимости системы. В теории чувствительности часто предполагают, что величины всех слагаемых под корнем в (2) имеют примерно одинаковый порядок (принцип равных влияний). Тогда вариация результирующего усилия, вызванная неточностью данных о жесткостных характеристиках,

Вариации результирующего усилия, вызванноая неточностью данных о жесткостных характеристиках

Величина φ_G зависит от двух факторов: степени статической неопределимости системы n (и, следовательно, от степени сложности расчетной модели) и величины ошибки каждого жесткостного параметра σ_о. То есть более детальная модель, чтобы обеспечить приемлемую ошибку результата, должна основываться на более точных исходных данных. В реальности это не всегда выполнимо и усложненная расчетная модель ведет к накоплению ошибок результатов расчета.

К этому следует добавить оценку вариации усилий, вызванную неточностью задания нагрузки, которая пропорциональна корню квадратному из общего числа параметров, с помощью которых описываются все компоненты нагрузки на систему. Эта оценка, как правило, также растет с увеличением размерности задачи.

Таким образом, вполне реальна угроза того, что потеря информации из-за неточности исходных данных может значительно превысить прирост информации за счет уточнения расчетной схемы.

Кроме жесткостей и нагрузок, неопределенными параметрами задачи являются и другие величины. В частности, одни из наиболее неопределенных и изменчивых — это условия сопряжения конструктивных элементов, которые чаще всего назначаются жесткими или шарнирными. В действительности имеет место некоторое промежуточное состояние. Например, согласно Еврокоду-3, в зависимости от значения взаимного угла поворота элементов узла при действии единичного момента узел может быть признан жестким, шарнирным или полужестким. В наших нормативных документах такая классификация отсутствует.

Хороший анализ работы конструкции должен учитывать это обстоятельство, например, путем выполнения расчетов по нескольким вариантам исходных данных с выбором «расчетного сочетания» не только для нагрузок, но и для жесткостных параметров. Конечно, это будет сверхосторожным подходом, поскольку вероятность наиболее неблагоприятного сочетания значений неопределенных параметров может оказаться столь мала, что позволит не принимать ее во внимание. Однако для целого ряда ответственных объектов такая проверка будет совсем не лишней.

Необходимо отметить, что оценки типа (2), как и другие оценки влияния разброса исходных данных, оказываются существенно завышенными при коррелированных ошибках входных параметров. Именно это обстоятельство меняет наше отношение к большеразмерным задачам, порождаемым конечно-элементным подходом к решению проблем механики сплошной среды, где параметры, описывающие конечные элементы, сильно коррелированы.

Сказанное выше ни в коей мере не следует понимать как панегирик «старым добрым временам», когда все решалось с использованием формулы М = qL²/8 и подсчетом на логарифмической линейке. Просто на смену бездумному усложнению расчетных схем должна прийти новая культура их использования, включающая в себя и оценку возможной неопределенности решения. Это станет реальным, когда разработчики программных систем сочтут, что без такой оценки результаты расчета представлять пользователю не следует. В качестве программы-минимум можно было бы предусмотреть возможность поиска невыгодного сочетания значений некоторых из входных параметров. Иначе еще долго будет поддерживаться уверенность, что в результате детального расчета получены объективные данные о напряженно-деформированном состоянии системы. А это иллюзия: в действительности мы имеем только одну из возможных реализаций значений усилий и перемещений, полученную на основе произвольно выбранного варианта неопределенной входной информации.

Отображение и контроль исходных данных

В задачах большой размерности резко возрастает вероятность появления ошибки в исходных данных. Исследования в инженерной психологии показывают приблизительно степенную зависимость вероятности человеческой ошибки от объема перерабатываемой человеком информации. На этом основании высказано предположение, что вероятность ошибки тесно связана с размером и сложностью рассматриваемой схемы конструкции.

Любой современный расчетно-вычислительный комплекс оперирует с достаточно разнородными данными, посредством которых описываются свойства конечных элементов, узлов, нагрузок и воздействий и т.п. При решении задач большой размерности одновременно рассматривать всю эту информацию трудно, а использовать стандартный подход, основанный на выделении фрагментов, не всегда удобно. В частности, это неудобство дает о себе знать при попытке проследить, как некоторый фактор соотносится с системой в целом (например, как в системе располагаются элементы, обладающие вполне определенной жесткостью).

Для решения такого рода задач в SCAD предусмотрены так называемые фильтры: с экрана монитора удаляется вся информация, которая в данный момент не представляет оперативного интереса. По отдельности и в любых комбинациях можно, например, отфильтровать информацию, касающуюся элементов определенного типа (стержни, пластины, оболочки) или занимающих определенное пространственное положение (вертикальные, горизонтальные). Можно включить или отключить отображение разного рода данных (узловые нагрузки, распределенные нагрузки, нумерации элементов и узлов, связи и др.). Широко применяется цветовая индикация данных одного типа, отличающихся только значениями. Всего в комплексе SCAD около сорока различных фильтров.

Рис. 1а. Использование фильтров: схема в целом	Рис. 1б. Использование фильтров: фильтр «Пластины»	Рис. 1в. Использование фильтров: фильтр «Цветовое отображение жесткостей»
Рис. 1 г. Использование фильтров: функция выделения только выбранных жесткостей	Рис. 1д. Использование фильтров: фрагментация не отфтильтрованных данных

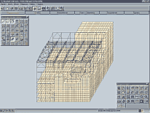
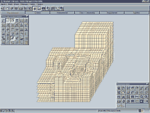
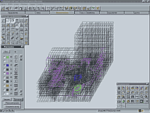
Типичный пример использования фильтрации представлен на рис. 1, где изображена схема части здания реакторного отделения АЭС. Показано, как по мере включения все новых фильтров постепенно сужается выводимый на экран компьютера объем информации. После включения фильтра «Цветовое отображение жесткостей» появляется возможность указать только часть информации (соответствующие цвета), сохраняемую для дальнейшей работы. Кроме того, эта информация может использоваться для выделения соответствующего фрагмента расчетной схемы — все остальное попросту исчезнет с экрана.

В комплексе SCAD реализовано несколько приемов декомпозиции расчетной схемы, что облегчает анализ задачи на входе и на выходе. Возможна декомпозиция по пространству (техника фрагментов), смыслу (техника групп) и структуре (техника подконструкций).

В роли фрагмента может выступить любая часть расчетной модели, которая была обозначена на экране «резиновым окном», после чего из нее автоматически удаляются элементы, попавшие в окно не полностью. Все прочие элементы расчетной схемы образуют фрагмент, и только они (естественно, до тех пор, пока это нужно) присутствуют на экране. К полученной части схемы может быть применена техника фильтрации, и наоборот — фрагментация возможна на отфильтрованном изображении. Таким образом, декомпозиция в технике фрагментов является только приемом для оперативного анализа информации.

Часто бывает необходимым зафиксировать некий фрагмент системы для многократного обращения к нему с различными запросами. Эта операция связана с использованием техники групп, с помощью которой любое подмножество объектов расчетной схемы (узлы, элементы, нагрузки) представляется как поименованная группа. Наконец, любая часть схемы может быть рассмотрена как подконструкция, а сама конструкция определена как совокупность подконструкций. Отличие группы от подконструкции в том, что последняя обладает свойством некой расчетной модели, а группа таковой не является.

Одновременное использование нескольких схем

Практически любой объект проектирования (за исключением простейших) в процессе расчета рассматривается с различных точек зрения; при этом было бы вполне естественным сопоставить подобному объекту не одну, а множество расчетных схем. Каждая из таких схем вносит свой вклад в понимание работы сооружения, и лишь их совокупность дает более или менее адекватное представление о действительном характере его несущей способности. При этом ряд простых расчетных моделей может дать более точное знание, чем одна сложная (переусложненная) расчетная схема, результаты расчета которой достаточно сложно осмыслить. На эту сторону проблемы указывал академик В.В. Новожилов, отмечая, что анализ результатов расчета по сложной модели напоминает обобщение и осмысление большого массива экспериментальных данных, а оценка явления в целом (с помощью простых расчетных моделей) позволяет с большим пониманием подойти как к построению, так и к анализу уточненной модели.

К сожалению, большинство современных программных систем мало приспособлено к такому режиму работы. Они не имеют ни понятийного, ни функционального инструментария для обмена информацией между несколькими параллельными расчетными моделями одного и того же объекта, не могут обмениваться результатами расчета таких моделей. Пожалуй, одно из немногих исключений — режим уточнения расчетной модели фрагмента, предусмотренный программным комплексом SCAD (речь об этом пойдет ниже), но этого явно недостаточно для полноценной реализации идеи одновременного использования различных схем.

Необходима возможность сопоставления результатов расчета по разным схемам. Такие оценки должны выполняться по разным типам результирующих данных как локально (поиск наибольших различий с указанием элементов или узлов системы, где они реализуются), так и «в среднем по области» (для схемы в целом, для фрагмента или подсхемы). Нам представляется, что здесь возможно использование техники нечетких множеств с лингвинистической переменной «степень соответствия», которой ставится в соответствие нечеткое множество, образованное лингвинистическими термами («высокая», «довольно высокая», «средняя», «довольно низкая», «низкая»). Тогда становится реальным создание экспертной системы, оперируя с которой расчетчик дает свои субъективные оценки «степени соответствия», а экспертная система на основе известных правил продукции приводит оценки степени правдоподобности и степени доверия к тем или иным компонентам результата расчета. На возможность использования экспертных систем при решении задач механики указано давно, однако практическая реализация идеи задержалась — не в последнюю очередь из-за традиционных подходов к расчету, поддерживаемых разработчиками программных средств.

Заметим, что возможность манипулирования спектром расчетных схем — действенное средство борьбы с переусложнением расчетов. Ведь супердетализация системы в целом — это зачастую реакция расчетчика на его потребность в точных данных по экстремальным результатам при отсутствии предварительной информации о месте появления такого результата. На всякий случай применяется детализированная расчетная схема, которая, возможно, позволит не пропустить искомый результат, хотя он может быть упущен из-за трудностей анализа и осмысления избыточной информации. Дело в том, что, начиная с некоторого уровня сложности системы, способность человека формулировать осмысленные и точные утверждения о ее поведении начинает резко падать: имеет место некоторый аналог принципа неопределенности Гейзенберга в отношении детальности и информативности результатов расчета, которые выступают в роли альтернирующих параметров.

Таким образом мы обозначили для разработчиков современных программных систем две взаимосвязанные задачи — создание аппарата для оперирования со многими расчетными схемами одного объекта и облегчение анализа результатов расчета сложной многоэлементной системы. В какой-то мере они дополняют друг друга и поодиночке проблему не решат.

Стоит отметить, что, имея дело с задачами большой размерности, расчетчик должен в известном смысле уподобиться художнику-карикатуристу, который воспроизводит оригинал не во всех деталях, подобно фотографическому аппарату, но упрощает и схематизирует его так, чтобы подчеркнуть наиболее характерные черты. Хорошая расчетная схема большой системы является лишь профессиональной «карикатурой» (или «дружеским шаржем»), утрирующей и подчеркивающей наиболее характерные свойства оригинала и игнорирующей все остальное. Наиболее полное и многостороннее представление, естественно, может быть получено в том случае, когда оригинал представлен целой серией карикатур.

Какие результаты требуются

Общепринятый набор разыскиваемых результатов (перемещения, усилия, поля напряжений) стал настолько традиционным, что почти не обсуждается. При этом он далеко не достаточен для серьезного осмысления характера полученного решения. Кроме того, способы отображения этих результатов весьма громоздки, что тоже не способствует ясному пониманию особенностей решенной задачи.

Результаты статического и динамического расчета сложной системы, представленные в числовой форме, являют собой такие огромные массивы данных, что их осмысление и анализ практически невыполнимы. Мало помогает и предусмотренная в большинстве программных систем возможность выборочной печати результатов, поскольку расчетчик не всегда знает, какие из них окажутся критическими.

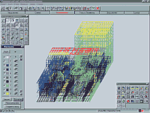
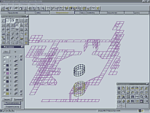
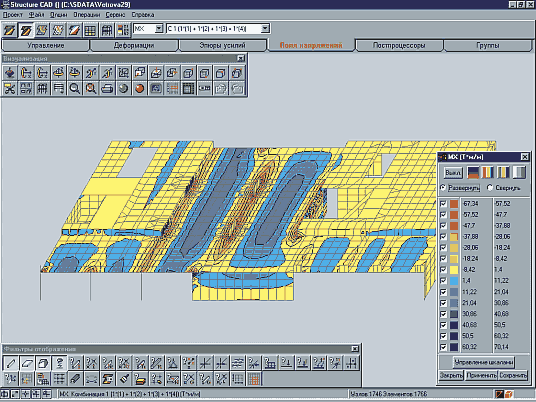
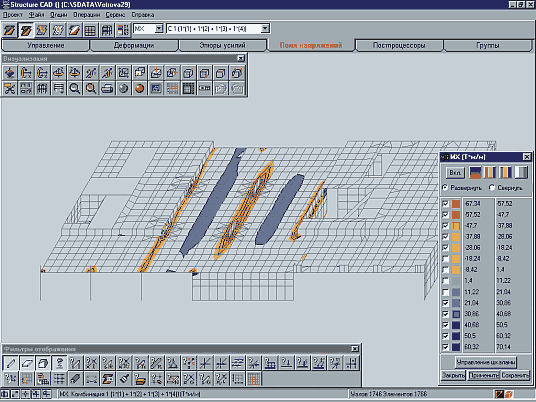
Несколько большую наглядность дает графическое отображение результатов в виде эпюров и изополей, при котором происходит серьезное сжатие информации. Впрочем, и это не всегда позволяет качественно произвести анализ, поскольку для системы в целом графическая информация может оказаться недостаточно разборчивой и удобочитаемой (рис. 2а). При ее фрагментации наглядность восстанавливается, но возникает новая проблема — поиск того фрагмента, на котором реализовались интересующие пользователя значения тех или иных результатов расчета.

Рис. 2а. Цветовое отображение информации (поля изгибающих моментов)

Выходом из положения может служить предложенный в комплексе SCAD прием, основанный на управлении цветовым отображением. Есть возможность выдавать в цвете только те части изополя, которые принадлежат определенному диапазону значений, отключив все прочие диапазоны (рис. 2б), — тогда становится очевидной локализация «критических» значений результатов расчета.

Рис. 2б. Цветовое отображение информации (поля изгибающих моментов)

Возможность найти и задокументировать требуемые результаты еще не решает проблему оценки результатов расчета.

Традиционно принято представлять результаты расчета (перемещения, усилия, напряжения) в некой «окончательной» форме, забывая обо всех погрешностях, присутствующих в исходной информации, а также о возможных погрешностях вычислений. Последнее особенно важно при решении нелинейных задач. Примером может служить реакция пользователей на присутствие в результатах нелинейного расчета значений невязки уравнений равновесия, соответствующих найденному приближенному решению. Эти данные, появившиеся в очередной версии программы (раньше они попросту не показывались), вызвали недовольство: пользователи сочли, что предыдущая версия работала точно, а новая — с ошибками.

Погрешность вычислений накапливается и при решении линейных задач большой размерности, поэтому комплекс SCAD выдает оценку точности разложения матрицы жесткости. Эта оценка оперирует с конкретной матрицей жесткости рассматриваемой системы и строится путем решения специальной вспомогательной задачи (тест А. Горбовца), для которой известно точное решение: все линейные перемещения равны единице, все углы поворота узлов — нулю. Максимальное отклонение от точного решения оценивает погрешность вычислений и дает возможность судить о корректности расчетной модели. Быть может, потому, что такая оценка выдается в протокол решения, а не в выходной документ с результатами расчета, неприятия пользователей она не вызвала. Но, к сожалению, неквалифицированные пользователи не всегда обращают внимание на эту оценку.

Традиция «точного» представления результатов расчета противоречит отмеченному выше свойству случайности исходных данных, которые, естественно, приводят и к случайному результату расчета. Поэтому в дополнение к оценке вычислительной погрешности необходима оценка возможного разброса результатов, связанного с неточностью входных параметров. Этими данными следовало бы дополнить традиционный набор результатов.

Кроме того, по мнению авторов, результаты нужно дополнить и анализом чувствительности решения к возможным изменениям основных параметров.

Другие проблемы

Требования и рекомендации по выбору расчетных моделей обычно обосновываются специальными исследованиями, результаты которых закрепляются традицией и практикой проектирования, а иногда отражаются в нормах проектирования. Этими же нормами могут быть определены и возможные конструктивные решения, обеспечивающие реализацию принятых расчетных предпосылок. К сожалению, эти положения не очень часто выполняются на практике. Требования норм, как правило, связаны с определенной расчетной моделью, но ее описание в нормативном документе не приводится, что создает ложное впечатление универсальности нормативного требования. Если при этом требование построено на использовании достаточно грубой расчетной модели, зачастую возникает парадоксальная ситуация: уточнение расчетной модели приводит к решениям менее экономичным, чем те, которые основаны на грубой модели нормативного документа.

По-видимому, оптимальный выход из рассматриваемой ситуации — установление некоторых правил обоснования расчетных моделей. Первый шаг в этом направлении сделан разработчиками Еврокода, в который включено специальное приложение с указанием правил обработки экспериментальных данных при обосновании значений тех или иных параметров, входящих в расчетные зависимости норм. Кроме того, Еврокод дает рекомендации относительно применения линейного или нелинейного расчета в зависимости от соотношения некоторых параметров конструкции.

Учесть эффекты геометрической и физической нелинейности для большинства используемых расчетных схем современных зданий и сооружений в принципе не очень трудно. Сложности начинаются после выполнения таких расчетов. Если не выполняется принцип суперпозиции, то неизвестно, что нужно делать с результатами нелинейных расчетов, выполненных для различных случаев нагружения системы. Выделить одно определяющее нагружение из множества возможных в большинстве случаев не удается (редкие исключения — например, конструкции плотины, где расчетное нагружение очевидно, — лишь подтверждают этот тезис). А систем, работающих только на один вариант нагружения, практически не бывает.

Таким образом, приходится мириться с тем, что большинство массовых расчетов будет выполняться по схемам, для которых адекватность реальной работе сооружения достаточно сомнительна, и необходимая «балансировка» будет достигаться использованием некоторых усредненных поправочных коэффициентов (таких, как коэффициент условий работы γ_с), значения которых обосновываются экспериментально. В этих условиях увлечение использованием переусложненных расчетных схем следует подвергнуть еще большему сомнению.

Возвращаясь к использованию результатов нелинейного расчета, отметим, что всякого рода нормативные проверки прочности и устойчивости элементов конструкций «с учетом пластической стадии работы», при которых используются усилия, найденные в результате упругого расчета системы, в значительной мере условны (по крайней мере для элементов статически неопределимых систем).

Аналогичное замечание относится и к использованию расчетных длин сжатых элементов, которые определяются путем расчета упругой системы на устойчивость. Насколько корректен такой бифуркационный расчет в упругой стадии по отношению к реальной работе конструкции, где на потерю устойчивости оказывают влияние совместные эффекты текучести материала и геометрической нелинейности, остается неясным. Вместе с тем от того, будет ли принят коэффициент свободной длины m равным 0,75 или 0,85, теоретическое значение несущей способности сжатого стального стержня зачастую зависит в большей степени, чем от величины коэффициента формы сечения h, с помощью которого учитывается неупругое выпучивание. После сказанного уже не кажутся парадоксальными результаты А.Я. Дривинга, показавшего на примере простой прямоугольной стержневой системы, что неучет предусмотренной СНиП II-23−81* пластической стадии работы материала при взятой из этих же норм завышенной расчетной длине, приводит к менее экономичному решению, чем упругий деформационный расчет системы, который определяет правильное значение расчетной длины стойки.

Заключение

Как утверждал один из основоположников кибернетики У. Эшби, есть определенные принципиальные ограничения по размеру задач, доступных для анализа, например число 10¹⁰⁰, которое равно произведению числа атомов во вселенной (10⁷³) на количество микросекунд существования земной коры (10²³), и «…возможность устранения этого ограничения менее вероятна, чем, например, возможность устранения ограничения, которое накладывается законом сохранения энергии… Я убежден, что в будущем теоретик систем должен стать экспертом по упрощению». Авторам остается только присоединиться к последнему призыву.

Экспертом по упрощению расчетных моделей может стать только высококвалифицированный специалист, а программная система разрабатывается в расчете на пользователей различной квалификации, что и вызывает некоторые из отмеченных выше противоречий. Возможным выходом из положения нам представляется принятое во многих компьютерных играх указание на уровень подготовки пользователя («Новичок», «Специалист», «Эксперт» и т.п.), при этом каждому уровню становится доступным тот или иной набор возможностей расчетного комплекса. Поскольку такое указание реализуется самим пользователем, негативная реакция на возможные ошибки при градации опыта должна быть исключена.

Помощь в правильной самоидентификации могла бы оказывать встроенная «экзаменующая» подсистема, построение которой отличалось бы от обычных систем типа «выбери ответ» тем, что среди предлагаемых ответов присутствовал не один, а несколько правильных — с характеристикой квалификации, соответствующей этому ответу, и необходимыми комментариями.

Скачать статью в формате PDF — 879.3 Кбайт